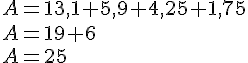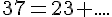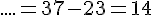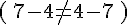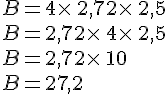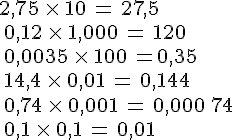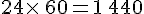Addition, soustraction, multiplication de deux nombres : cours de maths en 6ème à imprimer en PDF.
Mis à jour le 13 novembre 2025
Nous terminerons cette leçon avec des problèmes et leur résolution ainsi que les critères de divisibilité puis la division décimale et euclidienne. Cette leçon reprend toutes les notions du programme officiel de l’éducation nationale en maths et permet aux élèves de sixième d’assimiler le contenu de leur cours. L’élève sera, également, capable de donne des ordres de grandeurs ou de poser des opérations en colonne ou en ligne.
I. Addition de deux nombres décimaux
1.Vocabulaire et définition :
Exemple :
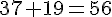
56 est la somme des termes 37 et 19.
Dans une addition, on a le droit :
- de regrouper les termes;
- de changer les termes de places.
On dit que l’addition est commutative.
ExempleS :
- Calculer astucieusement :
.
2. Calculer la somme suivante en ligne.
Nous allons utiliser la propriété de commutativité de l’addition pour calculer astucieusement cette somme.
3. Poser et calculer 1 856 + 525.
On place les chiffres les uns sous les autres, en commençant par les chiffres des unités.
Les nombres 1 856 et 525 sont les termes.
Le résultat 2 381 est la somme.
2. Calculs d’une somme en colonnes :
Remarque :
Il faut veiller à aligner chaque position du nombre l’une au dessus de l’autre.
3.Ordre de grandeur d’une opération :
Donner un ordre de grandeur du résultat d’une opération, c’est donner une approximation de ce résultat en effectuant un calcul beaucoup plus simple.
Exemple :
Donner un ordre de grandeur de la somme 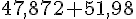
Nous avons 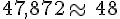
donc
.
Un ordre de grandeur de cette somme est donc 100.
II. Soustraction de deux nombres décimaux :
1.Définition et vocabulaire :
Exemple :
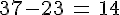
14 est la différence des termes 37 et 23.
Remarques :
- Ce résultat aurait pu être trouvé en complétant une addition à trous : si
- La soustraction n’est pas commutative, on ne peut pas modifier l’ordre des termes d’une soustraction
Exemple :
Poser et calculer 233 – 67.
On procède comme pour l’addition.
- Les nombres 233 et 67 sont les termes de la soustraction.
- Le résultat 166 est la différence.
Remarque :
On ne peut pas changer les termes de place dans une soustraction.
2. Calcul d’une différence en colonne :
Il faut veiller à aligner chaque position du nombre l’une au dessus de l’autre.
III. Multiplication de deux nombres décimaux :
1.Définition et vocabulaire
ExempleS :
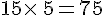
75 est le produit des facteurs 15 et 5.
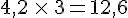
4,2 et 3 sont les facteurs et 12.6 est le produit.
Remarques :
– Lorsque l’on multiplie un nombre par 0, on obtient 0. de manière générale 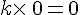
– Lorsque l’on multiplie un nombre par 1, on obtient ce nombre, de manière générale 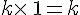
On peut modifier l’ordre des facteurs sans que cela ne modifie la valeur du produit
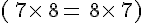
Exemple :
Cette propriété peut être utilisée pour calculer astucieusement un produit.
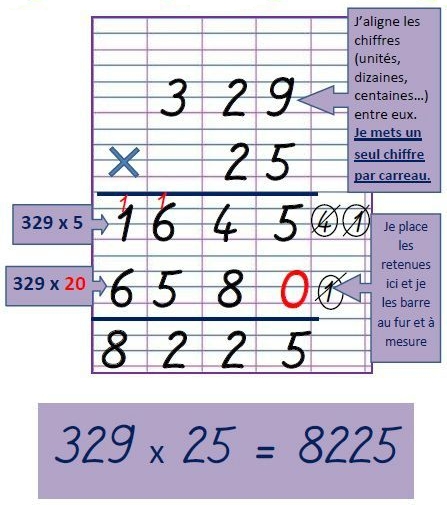
2.Calcul d’un produit en colonne :
Il faut veiller à aligner chaque position du nombre l’une au dessus de l’autre et de placer le plus grand nombre en premier afin que la multiplication contienne le moins de ligne possible.
Exemple :
Calculer le produit de 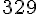
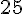
3.Multiplier par 10;100;1 000;0,1;0,01;0,001….
- Pour multiplier un nombre décimal par 10 ou 100 ou 1 000, il faut décaler la virgule de 1 rang ou 2 rangs ou 3 rangs vers la droite et compléter par des zéros si besoin.
- Pour multiplier un nombre décimal par 0,1 ou 0,01 ou 0,001, il faut décaler la virgule de 1 rang ou 2 rangs ou 3 rangs vers la gauche et compléter par des zéros si besoin.
Exemples :
Calculer les produits suivants :
4.Techniques opératoires
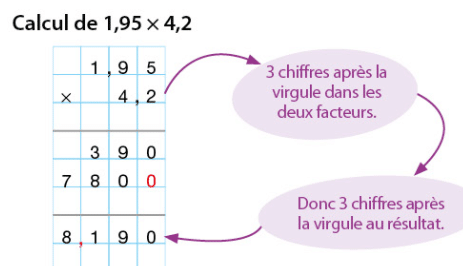
Pour effectuer la multiplication d’un nombre décimal par un nombre entier :
- on commence les calculs par la droite, sans tenir compte de la virgule;
- on place, dans le résultat, le même nombre de chiffres après la virgule que dans le nombre décimal.
Exemples :
Exemple :
Un ordre de grandeur de 1,95 est 2.
Un ordre de grandeur de 4,2 est 4; donc un ordre de grandeur de 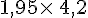
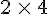
5.Priorités opératoires
- Les calculs entre parenthèses sont prioritaires;
- La multiplication est prioritaire sur les additions et les soustractions.
Exemples :
IV. Calculs avec les durées :
- 1 minute = 60 secondes
- 1 heure = 60 minutes =
secondes
- 1 jour = 24 heures =
secondes
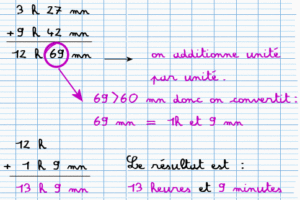
Exemple 1 :
Un livreur de marchandises effectue deux trajets. Le premier dure 3 h 27 min et le second dure 9 h 42 min.
Calculer la durée totale de son trajet.
Exemple 2 :
Un train part à 5 h 42 min de Lyon pour arriver à 9 h 16 min à Paris.
Quelle est la durée de ce trajet?
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «addition, soustraction, multiplication de deux nombres : cours de maths en 6ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Nos applications
Téléchargez la dernière version gratuite de nos applications.