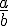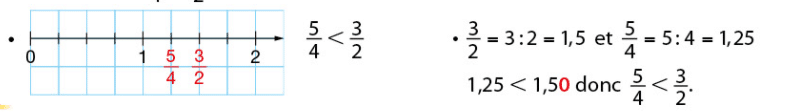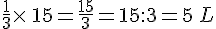Fractions : cours de maths en 6ème à imprimer en PDF.
Mis à jour le 19 janvier 2026
L’objectif sera, également, de savoir représenter graphiquement une fraction à l’aide de la notion de partage. L’élève devra connaître les différence entre une écriture fractionnaire, une fraction et une fraction décimale en sixième.
I. Définition :
Remarques :
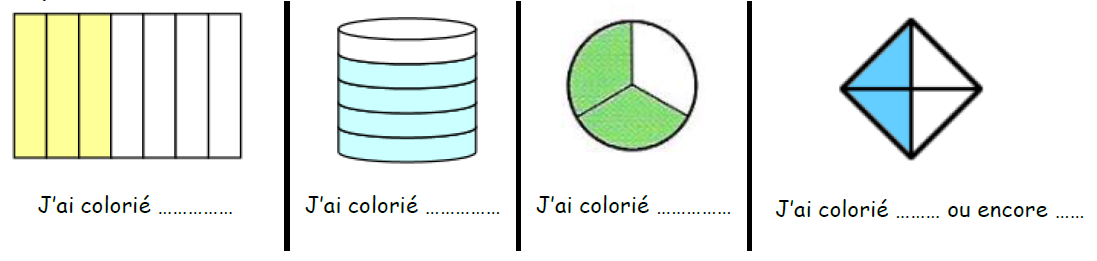
Pour chaque figure ci-dessous, quelle a été la fraction coloriée ?
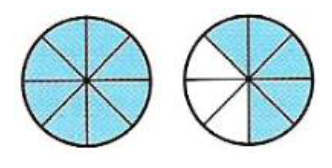
J’ai colorié 8 parties sur 8 mais aussi cinq parties sur un total de huit.
Soient a et b deux nombres entiers avec 
- La fraction
- a est appelé le numérateur de la fraction.
- b est appelé le dénominateur de la fraction.
Remarque :
- Une fraction est le quotient de deux nombres entiers.
- Si le numérateur et/ou le dénominateur est un nombre décimal alors on l’appelle écriture fractionnaire.
- Si le dénominateur est 1,10,100,… alors on l’appelle fraction décimale.
Exemples :
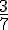
Cela veut dire que l’on coupe notre figure en sept parts égales et nous prenons 3.
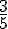
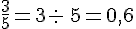
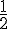
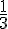
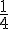
Exercices :
Placer sur la demi-droite graduée les nombres :
II. Fractions et quotients
1.Définition et vocabulaire
Exemple :
Ce rectangle représente l’unité; on le partage en quatre parts égales.
Chaque partie représente la fraction 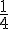
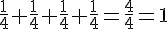
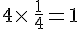
2. Placement et comparaison sur une demi-droite graduée
Exemple :
Pour placer le nombre 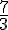
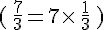
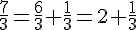
3. Quotient
III. Les fractions égales :
On ne change pas la valeur d’une fraction en multipliant ( ou en divisant) le numérateur et le dénominateur par un même nombre non nul.
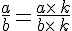
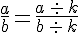
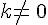

Exemples :
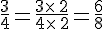
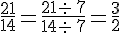
Exemples :
Simplifier les fractions suivantes :
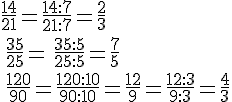
IV. Prendre une fraction d’une quantité :
Prendre une fraction d’une quantité revient à multiplier cette fraction par cette quantité.
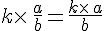
Exemple :
Dans une société de 32 employés, 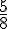
Combien de salariés portent des lunettes ?
Il faut calculer 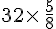
Première méthode :
On commence par la multiplication :
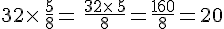
Seconde méthode :
On commence par la division :
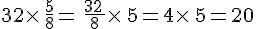
Troisième méthode :
On calcule la fraction si c’est un nombre décimal :
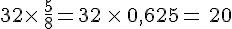
Conclusion :
Cette société comporte 20 employés qui portent des lunettes.
V. Propriétés des fractions
1.Egalités de fractions simples
Exemple 1 :
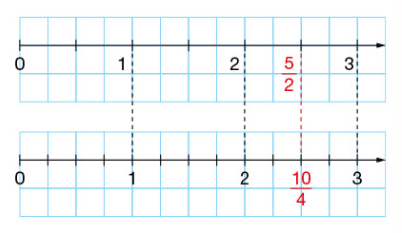
On a placé le nombre 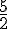
On partage l’unité en deux fois plus de parts; on prend alors deux fois plus de parts
et donc 
Exemple 2 :
Voici différentes fractions égales à 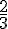
2.Comparaison et demi-droite graduée
Exemple 1 :
Sur cette demi-droite graduée, 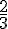
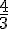
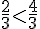
Exemple 2 :
Pour comparer 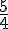
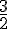
3.Prendre une fraction d’une quantité
Exemples :
- Prendre
- Prendre
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «fractions : cours de maths en 6ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 6ème
Exercices de 6ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.