Parallélogramme : cours de maths en 5ème à imprimer à télécharger en PDF
I Définitions et vocabulaire :
1. Rappels :
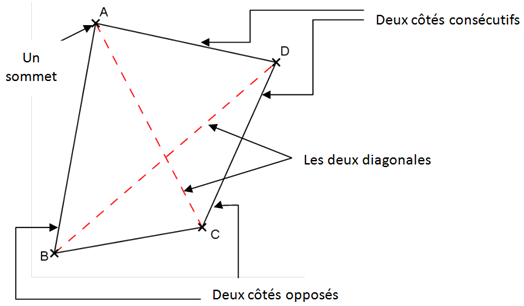
Un quadrilatère est une figure géométrique qui possède 4 côtés. Les points A,B,C et D sont appelés les sommets du quadrilatère.
Les côtés qui sont en face l’un de l’autre s’appellent les côtés opposés.
Les côtés qui se suivent (un sommet en commun) sont appelés les côtés consécutifs.
Les segments qui relient deux sommets opposés sont appelés les diagonales du quadrilatère.
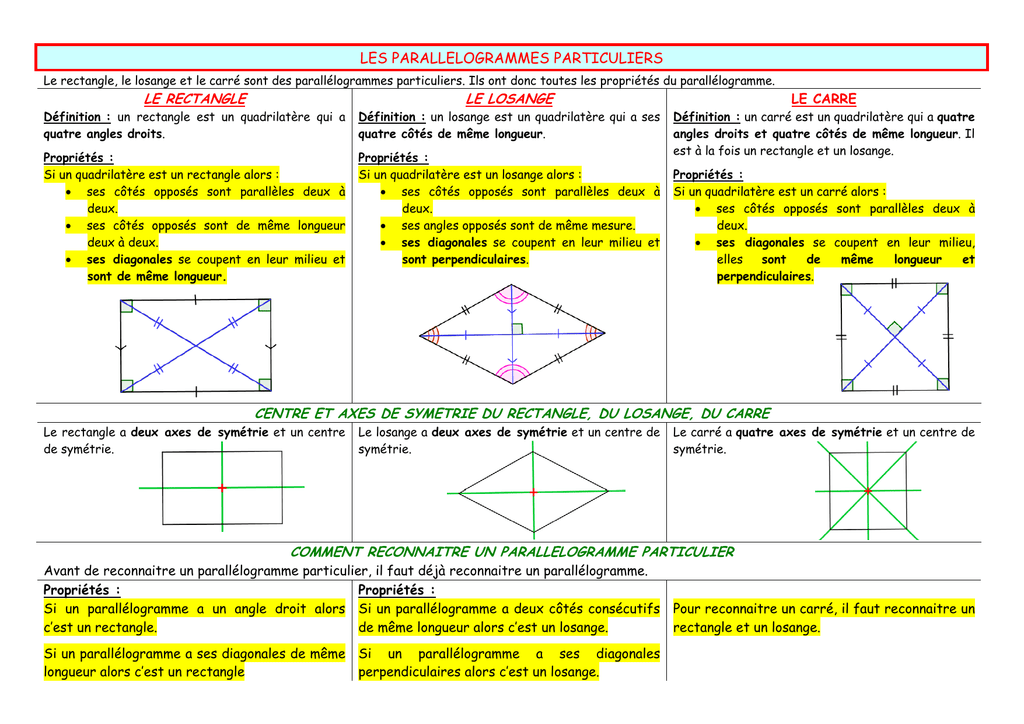
II. Le parallélogramme et ses propriétés :
1.Définition et vocabulaire :
2.Les propriétés du parallélogramme :
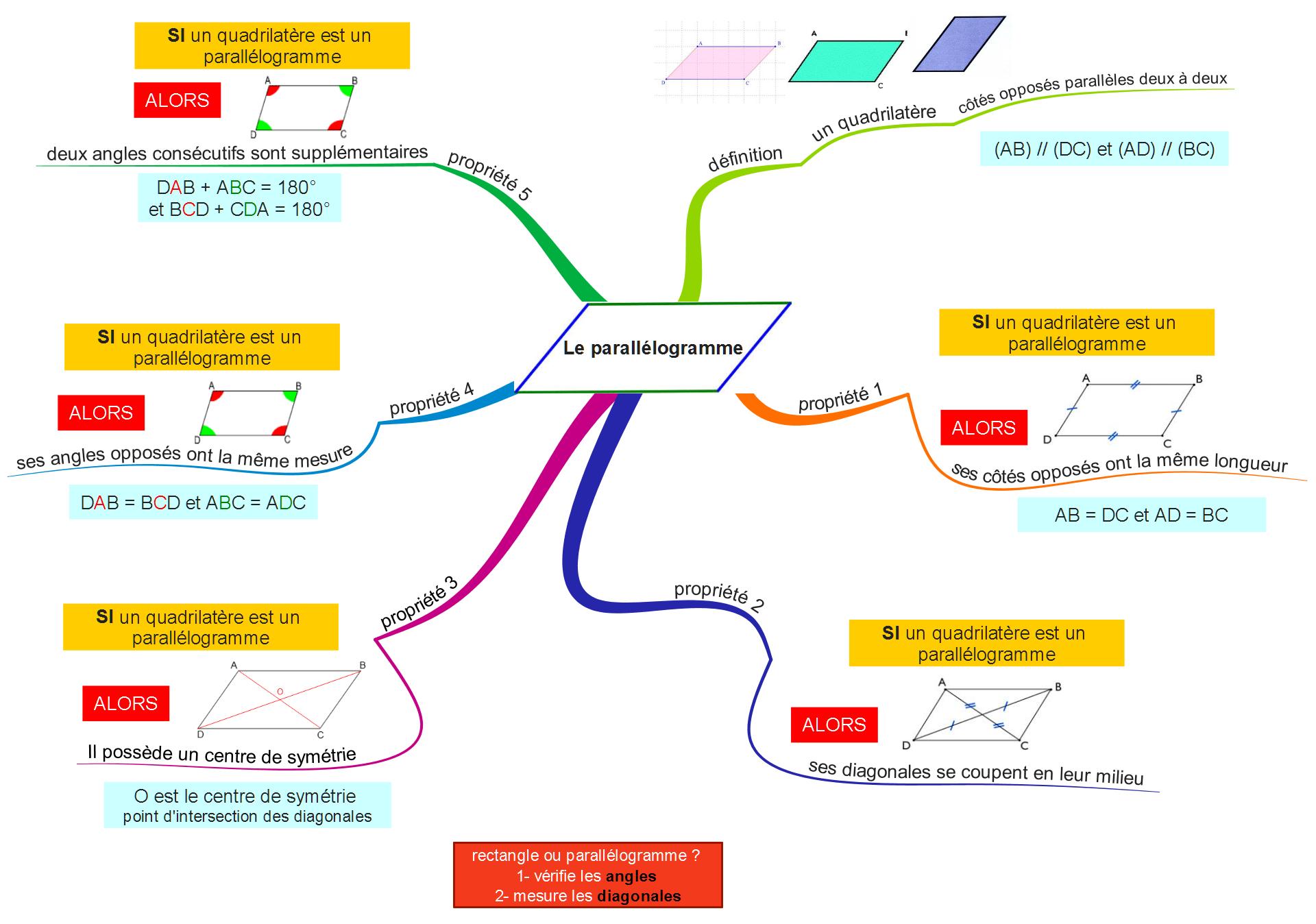
Dans un parallélogramme, les côtés opposés sont parallèles deux à deux.Nous avons (AB)//(DC) et (AD)//(BC).
Preuve :
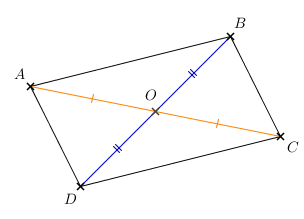
Nous savons que le point O est le centre de symétrie du parallélogramme.
Or, la symétrie centrale transforme une droite en une droite qui lui est parallèle.
Les droites (AB) et (CD) sont symétriques (de même pour (AD) et (BC)),
on en déduit que (AB)//(DC) et (AD)//(BC).
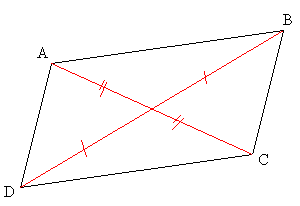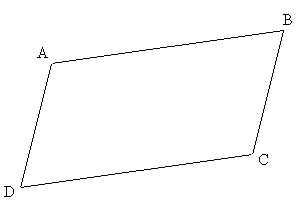
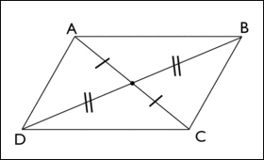
Dans un parallélogramme, les côtés opposés ont la même longueur.Nous avons AB=DC et AD=BC.
Preuve :
Dans un parallélogramme, le point d’intersection O des diagonales est son centre de symétrie.
Or, la symétrie centrale conserve la longueur des segments.
Les segments [AB] et [DC] sont symétriques par rapport à O (de même pour [AD] et [BC]).
On en déduit que AB=DC et AD=BC.
Méthode de construction :
Nous utilisons la propriété précédente pour construire un parallélogramme à la règle et au compas.
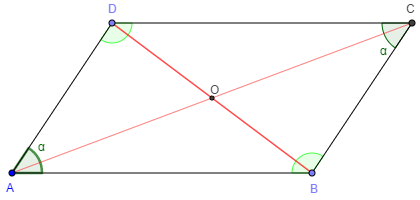
Dans un parallélogramme, les angles opposés ont la même mesure.Nous avons : 
et 
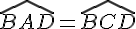
Preuve :
Le point O d’intersection des diagonales est le centre de symétrie du parallélogramme.
Or, la symétrie centrale conserve la mesure des angles.
Les angles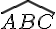 
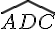
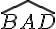
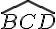
On en déduit que et
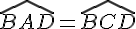
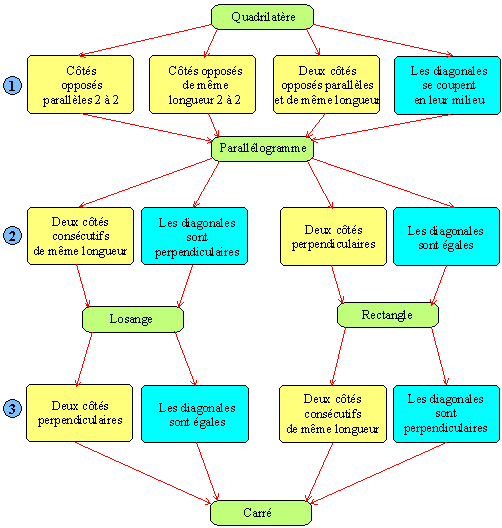
III. Les parallélogrammes particuliers :
Synthèse :
Applications :
Ces affirmations sont-elles vraies ou fausses ?
- Un parallélogramme a deux axes de symétrie.
- Si E et F sont les symétriques respectifs de G et H par rapport à ,alors EFGH est un parallélogramme de centre O.
- Un parallélogramme a quatre angles égaux.
- Si un quadrilatère a trois angles droits, alors c’est un rectangle.
- Si un quadrilatère a trois côtés égaux, alors c’est un losange.
IV. Carte mentale sur les parallélogrammes :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «parallélogramme : cours de maths en 5ème à imprimer à télécharger en PDF» au format PDF afin de pouvoir travailler en totale autonomie.
