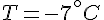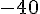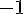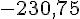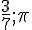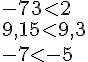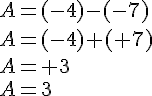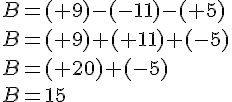Les nombres relatifs : cours de maths en 5ème à imprimer en PDF.

Mis à jour le 8 mars 2025

Sommaire

Les nombres relatifs avec un cours de maths en 5ème en PDF. L’élève devra connaître la définition avec la partie numérique et son signe. L’ojectif sera de comparer des nombres relatifs mais également, les ranger dans un ordre croissant ou décroissant. Nous nous placerons dans un repère orthonormé du plan afin de placer des points à partir de leurs coordonnées (abscisse et ordonnée) en cinquième.

I Introduction aux nombres relatifs :

1.Activité d’introduction :

2.Définitions et vocabulaire :

Définition :

Nous découvrons un nouvel ensemble de nombres, les nombres relatifs.

Il en existe deux sortes :

les nombres relatifs positifs : $+7;+123,42;+\pi;0$ .
les nombres relatifs négatifs : $-1,4;-\frac{2}{3};-\pi;-789,569;0$ .

Remarque :

Le chiffre zéro est le seul nombre relatif à la fois positif et négatif.

Ces nombres relatifs, vous les avez déjà rencontrés dans de nombreuses situations de la vie de tous les jours.

Exemples :

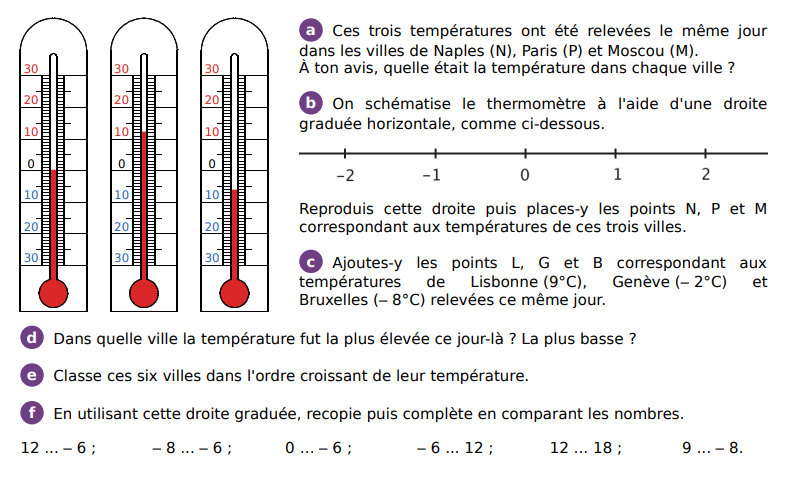
les températures en hiver : $T=-7^{\circ}C$ ;
les dates en histoire : ;
les ascenseurs : étage ;
les comptes bancaires : €.

Remarque :

Votre calculatrice connait les nombres relatifs et elle sait également effectuer des calculs contenant des nombres relatifs.

II. Repérage sur une droite graduée et nombres relatifs :

Définition :

Une droite graduée est une droite comportant une origine O et sur laquelle on reporte une unité.

Propriété :

Tout point d’une droite graduée peut être représenté par un nombre relatif qui est appelé l’abscisse du point.

Exemple :

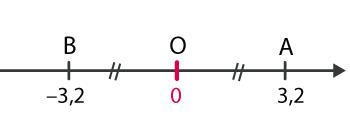
Sur la droite graduée précédente, le point A a pour abscisse -1, on note .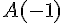

se lit le point B d’abscisse 5.

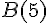
L’origine de la droite graduée O a pour abscisse zéro. On note .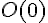

Définition :

La distance OB est la distance à zéro du nombre relatif 5 (de même 1 est la distance à zéro du nombre relatif -1).

Définition :

Tout nombre relatif est composé de deux éléments :

son signe (+ ou -);
sa partie numérique ( ou distance à zéro).

Définition :

On appelle nombres opposés, deux nombres relatifs tels que :

leurs signes sont différents;
leur partie numérique sont égales.

Exemples :

Les nombres relatifs 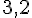et sont des nombres opposés et les points qui les représentent sur une droite graduée sont symétriques par rapport au point O (origine).

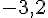
III Comparaison de nombres relatifs :

Remarque :

Si nous représentons deux nombres relatifs sur une droite graduée alors celui qui est le plus grand est celui qui est situé le plus à droite sur la droite graduée.

Propriété :

Considérons deux nombres relatifs.

Si les deux nombres relatifs sont de signes différents alors le plus grand est celui qui est positif.
Si les deux nombres relatifs sont positifs alors le plus grand est celui qui a la plus grande partie numérique.
Si deux nombres relatifs sont négatifs alors le plus grand est celui qui a la plus petite partie numérique.

Exemples :

$-73<2\\9,15<9,3\\-7<-5$

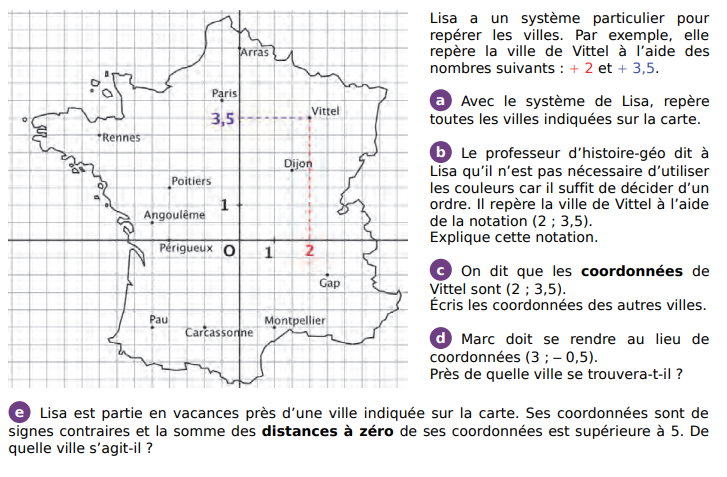
IV. Repérage dans le plan :

1.Activité d’introduction :

2.Coordonnées d’un point dans un repère :

Définition :

Un repère orthogonal du plan est la donnée de deux droites graduée perpendiculaires de même origine O. La droite graduée horizontale est appelée l’axe des abscisses et la droite graduée verticale est l’axe des ordonnées.

Moyen mnémotechnique :

Un moyen mnémotechnique pour ne pas confondre le nom de ces deux axes : la première lettre du mot ordonnée est la lettre O donc l’axe des ordonnées est l’axe dirigé vers le haut.

Propriété :

Tout point du plan peut être repéré par un couple de nombres relatifs appelé coordonnées du point.
La première valeur est appelée l’abscisse du point;
La seconde valeur est appelée l’ordonnée du point.

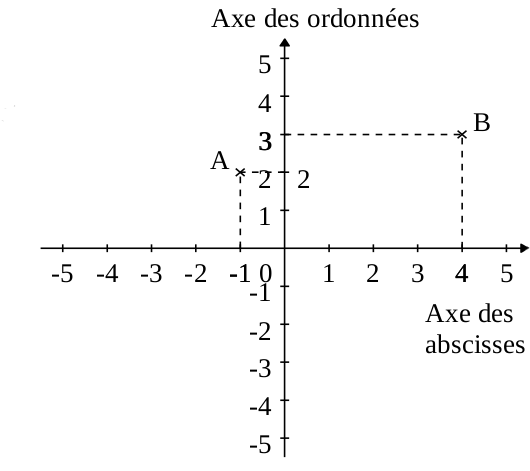
Exemple :

Dans le repère suivant:

Le point A a pour coordonnées : .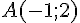

Le point B a pour coordonnées : .

V. Addition et soustraction de nombres relatifs :

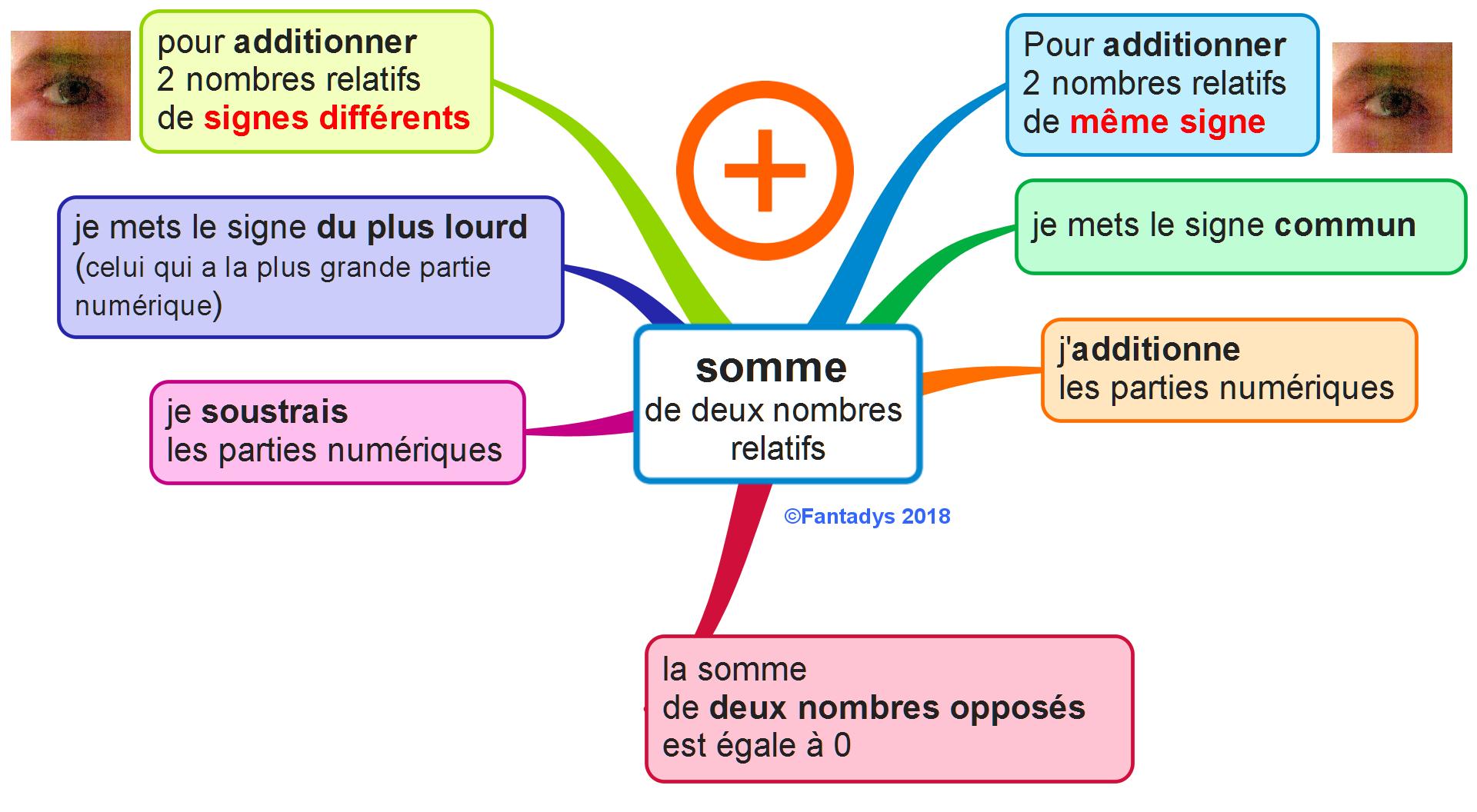
1. Somme de deux nombres relatifs :

Propriété 1 :

Considérons deux nombres relatifs.Pour effectuer la somme de deux nombres relatifs ayant le même signe :

on conserve le signe en commun;
on additionne les parties numériques.

Exemples :

Calculer les sommes suivantes :

$A=(+3)+(+7)\\A=+10$ $B=(-3)+(-17)\\B=-20$

Propriété 2 :

Considérons deux nombres relatifs.Pour effectuer la somme de deux nombres relatifs ayant des signes différents :

on conserve le signe du nombre ayant la plus grande partie numérique;
on effectue la différence positive des parties numériques.

Exemples :

Calculer la somme des nombres relatifs :

$A=(+3)+(-7)\\A=-4$ $B=(-3)+(+17)\\B=+14$

Remarque :

Par la suite, nous ne noterons pas le signe + en début de ligne.

2.Carte mentale pour l’addition de deux nombres relatifs :

3.Différence de deux nombres relatifs :

Propriété :

Soustraire un nombre relatif, c’est ajouter son opposé.

Remarque :

Pour effectuer la soustraction de deux nombres relatifs, nous transformons la soustraction en addition puis, nous utilisons les propriétés abordées précédemment.

Exemples :

Calculer les expressions suivantes :

$A=(-4)-(-7)\\A=(-4)+(+7)\\A=+3\\A=3$

$B=(+9)-(-11)-(+5)\\B=(+9)+(+11)+(-5)\\B=(+20)+(-5)\\B=15$

4.Carte mentale pour la soustraction de deux nombres relatifs :

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «les nombres relatifs : cours de maths en 5ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Vous n'avez pas consulté ces documents :

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 13 324 139 cours et exercices de maths téléchargés en PDF et 4 250 exercices.