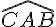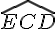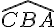Les angles : cours de maths en 5ème à imprimer en PDF.
Mis à jour le 25 janvier 2026
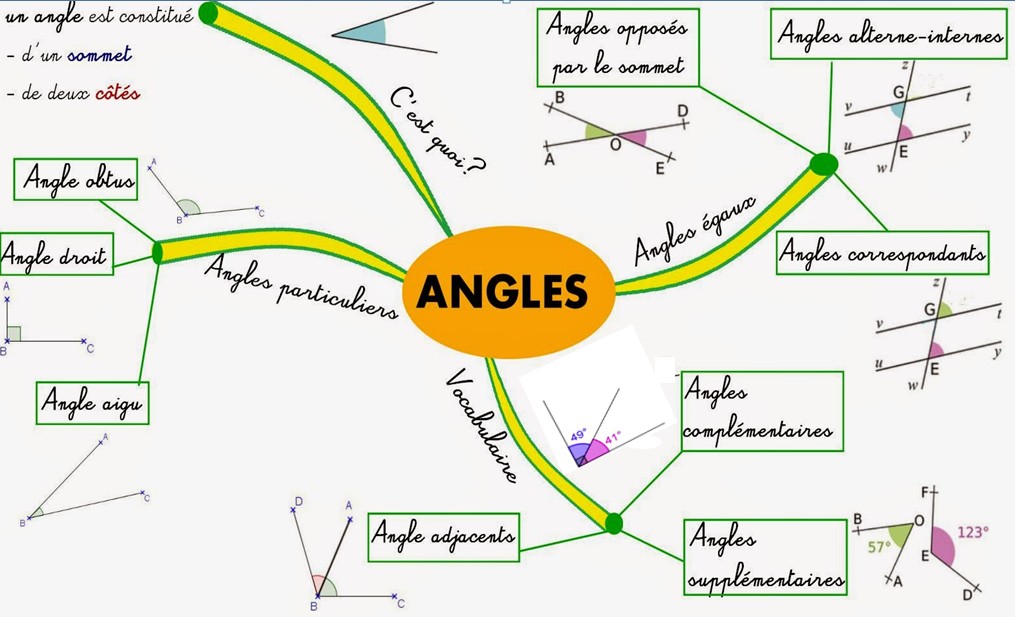
I. Les différents angles et leurs propriétés :
1.Les angles adjacents :
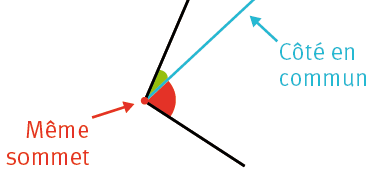
Deux angles sont adjacents lorsqu’ils :
- ont le même sommet;
- ont un côté en commun;
- sont situés de part et d’autre du côté en commun.
Exemples :
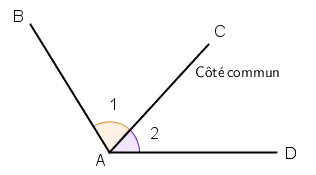
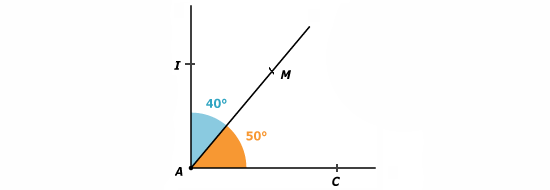
Les angles 
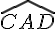
- ils ont le sommet A en commun;
- ils ont le côté (AC) en commun;
- ils sont situés de part et d’autre du côté en commun (AC).
Les angles 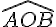
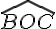
Remarque:
Les angles adjacents 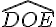
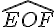
2.Les angles opposés par le sommet :
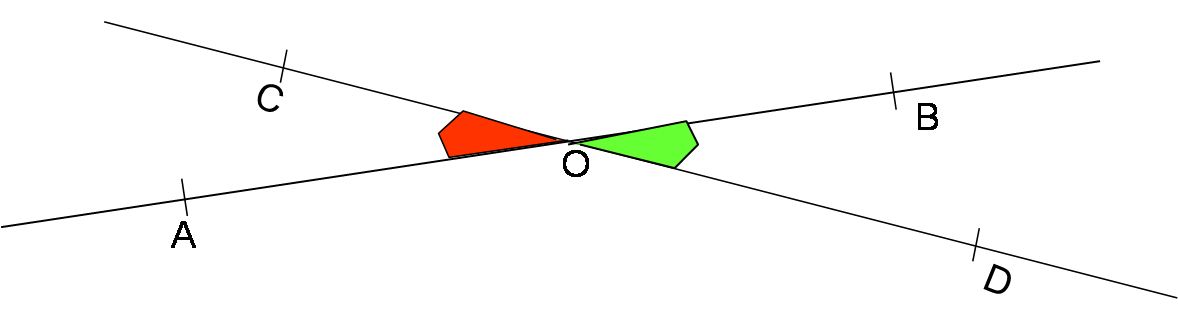
Deux angles sont opposés par le sommet si :
- ils ont le même sommet;
- Les côtés de l’un sont le prolongement des côtés de l’autre.
Exemple :
Les angles 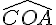

- ils ont le point O comme sommet en commun;
- ils ont leur côtés (CD) et (AB) en commun.
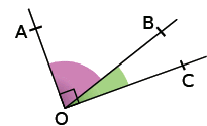
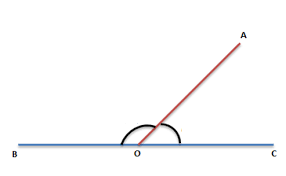
3.Les angles complémentaires :
Exemple :
Les angles 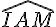
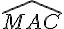
.
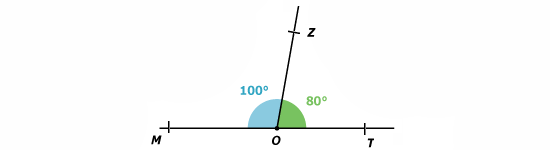
4.Les angles supplémentaires :
Exemple :
Les angles 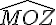
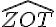
.
II.Les angles définis par deux droites et une sécantes :
1.Définitions et vocabulaire :
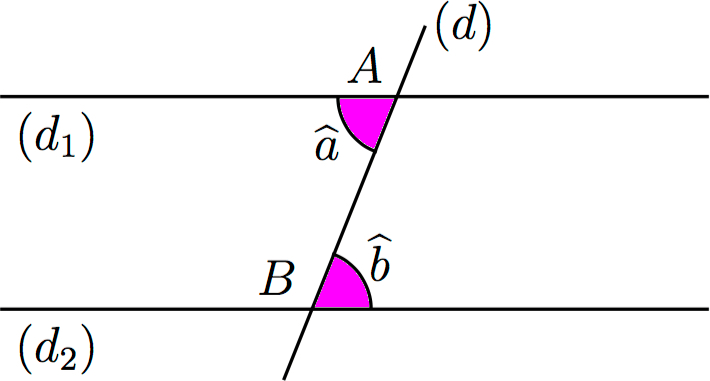
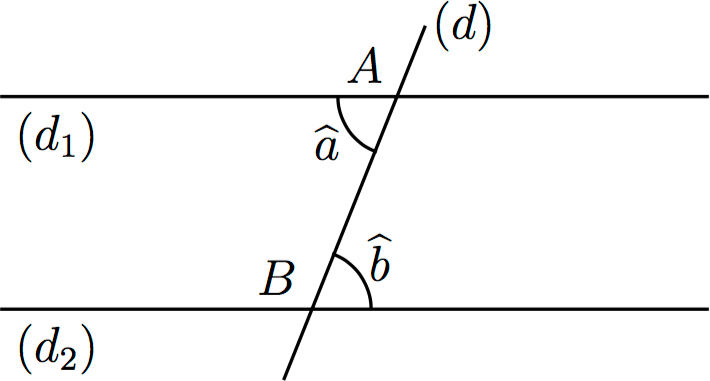
On considère deux droites 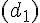
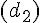
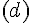
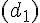
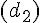
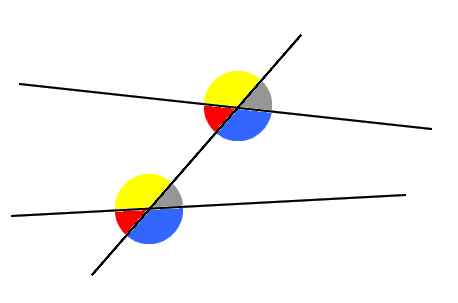
Deux angles sont dits alternes-internes si :
- ils sont situés entre
- ils sont de part et d’autre de
Les angles 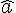
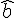
On considère deux droites 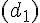
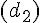
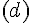
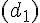
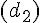
- les deux angles sont situés au-dessus (ou au-dessous) de
- ils sont du même côté de
Chaque couple d’angles colorés ci-dessus sont correspondants.
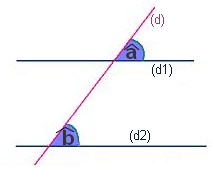
2.Cas où les deux droites sont parallèles :
Si deux angles alternes-internes sont définis par deux droites parallèles alors ces deux angles ont la même mesure.Si 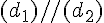
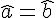
Si deux angles correspondants sont définis par deux droites parallèles alors ces deux angles ont la même mesure.Si 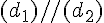
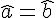
3.Cas où deux angles sont égaux :
Si deux angles alternes-internes ont la même mesure alors ils sont définis par deux droites parallèles.Si 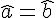
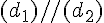
Si deux angles correspondants ont la même mesure alors ils sont définis par deux droites parallèles.Si 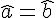
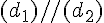
Exemple :
Les angles 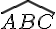
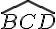
De plus, le codage indique qu’ils ont la même mesure. Donc les droites (AB) et (CD) sont parallèles.
Exemple :
On sait que les droites (AB) et (CD) sont parallèles.
- Les angles correspondants
.
- Les angles alternes-internes
.
III.Carte mentale sur les angles :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «les angles : cours de maths en 5ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Exercices de 5ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.