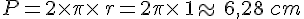Prisme droit et cylindre : cours de maths en 5ème sur les volumes de solides à imprimer en PDF.
Mis à jour le 20 décembre 2025
I. Le prisme droit :
1.Définition et vocabulaire :
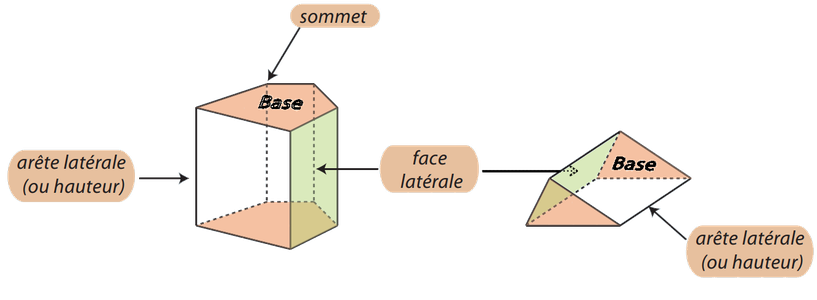
Un prisme droit est un solide ayant :
- deux bases qui sont des polygones parallèles et superposables;
- des faces latérales qui sont des rectangles perpendiculaires aux bases.
La hauteur d’un prisme droit est la longueur d’une des arêtes latérales.
Remarque :
Il ne faut pas confondre prisme droit et pavé droit (parallélépipède rectangle).
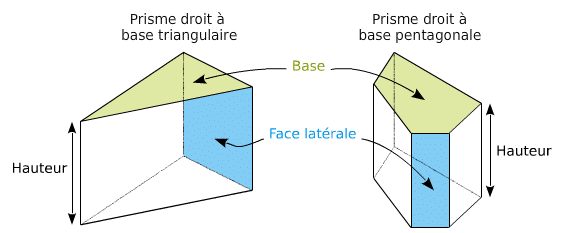
- La base du premier prisme est un triangle
- Il a cinq faces dont trois faces latérales, 9 arêtes et six sommets.
- La base du second prisme est un pentagone.
- Il a 7 faces dont 5 faces latérales, 15 arêtes et dix sommets.
Remarque :
- Toutes les faces latérales ont une dimension commune : la hauteur du prisme.
- Le nombre de faces latérales est égal au nombre de côtés de la base.
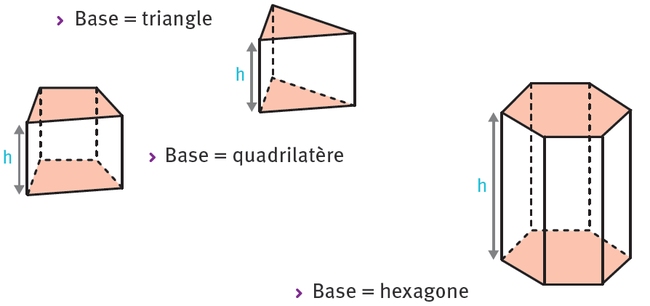
2.Exemples de prismes droits :
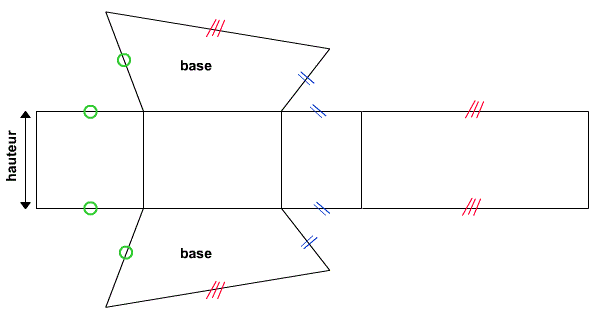
3.Le patron d’un prisme droit :
Exemples :
Le patron d’un prisme droit à base triangulaire.
Le patron d’un prisme droit dont la base est un quadrilatère.
4.le volume d’un prisme droit :
Considérons un prisme droit de base B et de hauteur h.
Son volume est donné par la formule suivante :
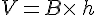
II. Le cylindre de révolution :
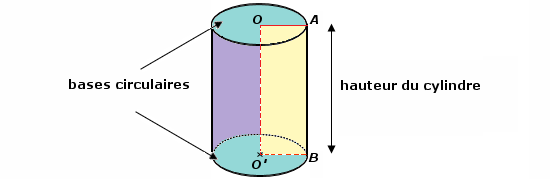
1.Définition et vocabulaire :
Un cylindre de révolution est constitué de ses deux bases qui sont des disques et de la surface latérale qui est un rectangle.
Les deux bases sont deux disques parallèles et superposables, qui ont le même rayon R.
Remarque :
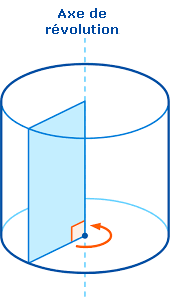
Le cylindre est généré (créé) en effectuant la rotation d’un rectangle par rapport à un axe.
En sciences physiques, un mouvement de rotation s’appelle une révolution.
2.Le patron d’un cylindre de révolution :
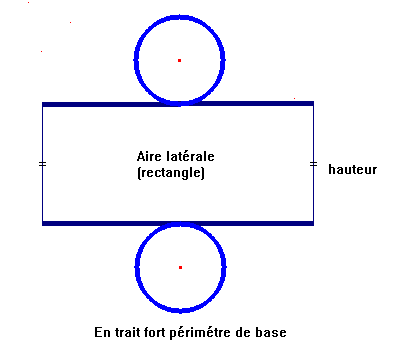
Le patron d’un cylindre de révolution est constitué de ses deux bases (disques) et de la surface latérale qui est un rectangle.
Exemple :
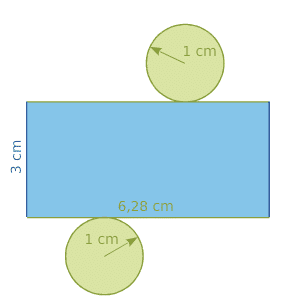
Voici le patron d’un cylindre de révolution de hauteur 3 cm ayant pour base un disque de rayon 1 cm.
La surface latérale de ce cylindre est un rectangle :
- qui a pour largeur la hauteur du prisme soit 3 cm.
- qui a pour longueur le périmètre du disque de base soit
3.le volume d’un cylindre :
Considérons un cylindre de base B, un disque de rayon R, et de hauteur h.
Son volume est donné par la formule suivante :
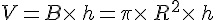
Exemple :
Calculer le volume d’un cylindre dont la base a un rayon de 5 cm et une hauteur de 7 cm.
Arrondir le résultat au dixième.
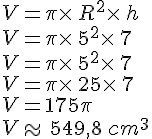
III. Les sections de solides et volumes
Exemple :
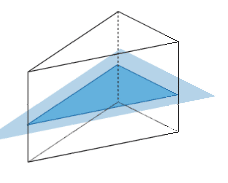
On coupe un prisme à base triangulaire par un plan parallèle à sa base.
La section est un triangle identique au triangle de base.
remarque :
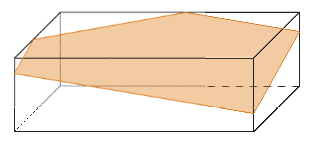
Les pavés sont des prismes particuliers, pour lesquels la section d’un plan parallèle à la base est un rectangle identique à cette base.
Exemple :
On coupe un cylindre de révolution de hauteur 4 cm dont le rayon de la base est 1 cm, par un plan perpendiculaire à son axe.
La section est un disque de rayon 1 cm.
Exemple :
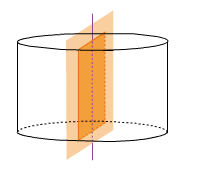
On coupe un cylindre de révolution de hauteur 5 cm, dont le rayon de la base est 2 cm, par un plan contenant son axe.
La section est un rectangle de longueur la hauteur du cylindre : 5 cm et de largeur le diamètre de la base : 4 cm.
IV: Calcul de volumes de solides
Pour calculer le volume V d’un prisme droit ou d’un cylindre de révolution, on multiplie l’aire d’une base par sa hauteur h.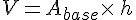
Exemple :
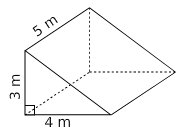
Un grenier a la forme d’un prisme droit à base triangulaire. On veut calculer son volume.
On calcule l’aire d’une base qui est un triangle rectangle :
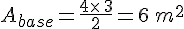
On multiplie l’aire d’une base par la hauteur :
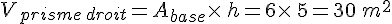
Le volume de ce grenier est de 30 m².
Exemple :
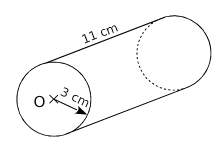
Une canette a la forme d’un cylindre de révolution.
On veut calculer sa contenance en centilitres.
On calcule l’aire d’une base qui est un disque de rayon 3 cm.
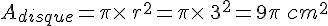
On multiplie l’aire d’une base par sa hauteur qui est de 11 cm.
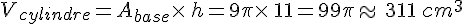
Le volume de cette canette est d’environ 311 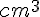
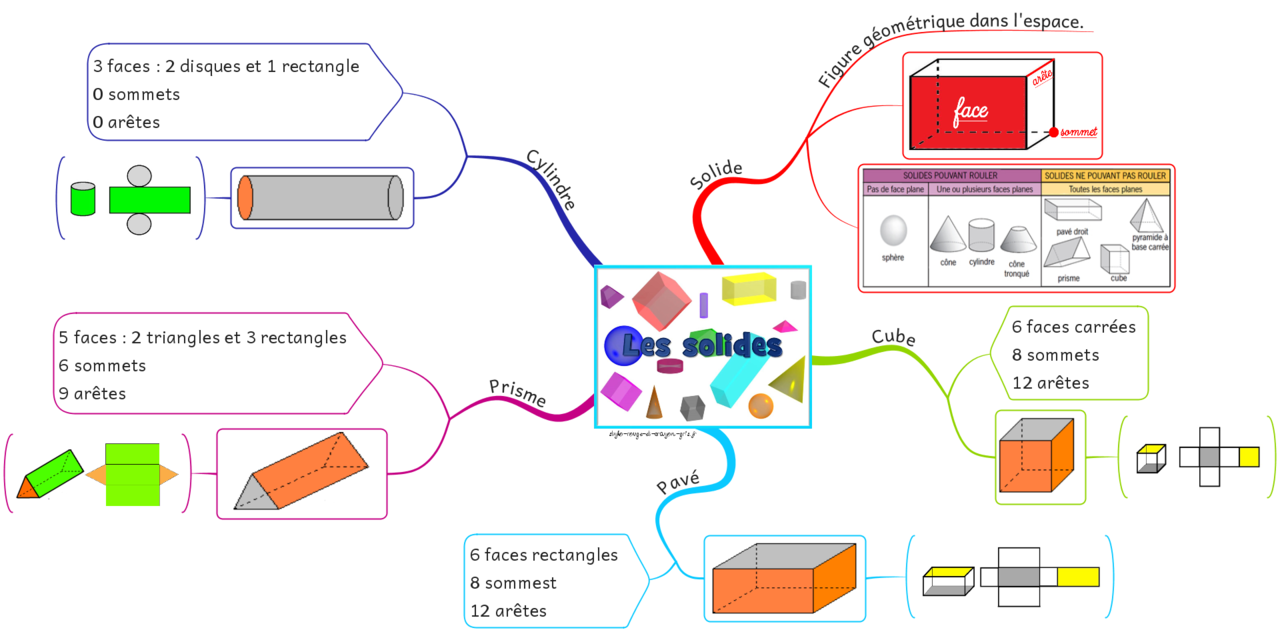
V. Carte mentale sur le prisme droit et le cylindre de révolution :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «prisme droit et cylindre : cours de maths en 5ème sur les volumes de solides à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Exercices de 5ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.