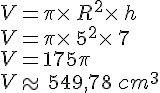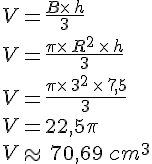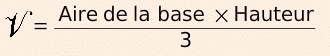Pyramides, cônes et volumes de solides : cours de maths en 4ème à imprimer en PDF.

Mis à jour le 20 décembre 2025

Sommaire

📚Cours de Mathématiques4ème • collège

Pyramides, cônes et volumes de solides

⏱️Temps de lecture : 6 min

🎯Difficulté : Intermédiaire

📚Cycle 4

📋Prérequis : Programme 5ème maîtrisé

📄Format PDF disponible gratuitement

Les pyramides les cônes de révolution avec un cours de maths en 4ème complet qui vous permettra de connaître des les différents solides et de calculer leur volume.En géométrie, un solide est un objet de l’espace qui a une longueur, une largeur et une hauteur ou une profondeur. Les solides occupent l’espace et ont un volume défini, et ils sont souvent composés de formes bidimensionnelles appelées faces. L’élève devra être capable de représenter un solide en perspective cavalière mais, également, savoir tracer son patron. Calculer des volumes en appliqua,t les formulés et en sachant effectuer des conversions pour le cube, le pavé droit, le cylindre, la pyramide et le cône de révolution. Un autre but de cette leçon et de résoudre des problèmes concrets en quatrième.

I. Les solides sans pointe :

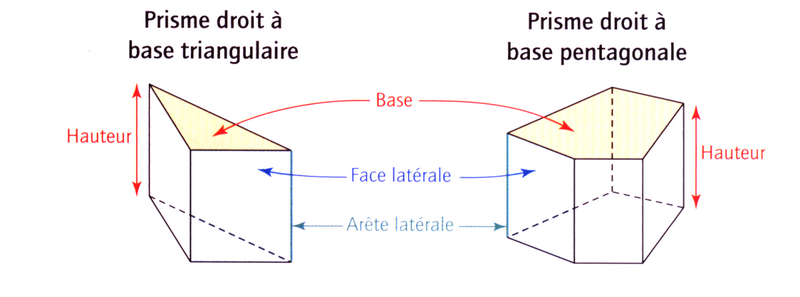
1.Le prisme droit :

Définition :

Un prisme droit est un solide qui a une base qui est un polygone et des faces latérales qui sont des rectangles.

Remarque :
Le cube est un prisme droit particulier.

Il ne faut pas confondre prisme droit et pavé droit (parallélépipède rectangle).

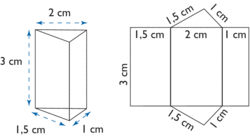
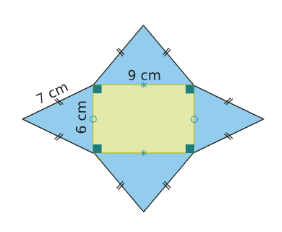
2.Patron d’un prisme droit :

3.Volume du prisme droit :

Propriété :

On considère un prisme droit de base B et de hauteur h.

Son volume est donné par la formule :

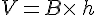
$V=B\times\,h$ .

Exemple :

Soit un prisme droit dont la base du prisme est un triangle de base 6 cm et de hauteur 4 cm, et si la hauteur du prisme est de 8 cm alors son volume est :

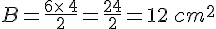
$B=\frac{6\times\,4}{2}=\frac{24}{2}=12\,cm^2$ et $V=B\times\,h=12\times\,8=96\,cm^3$

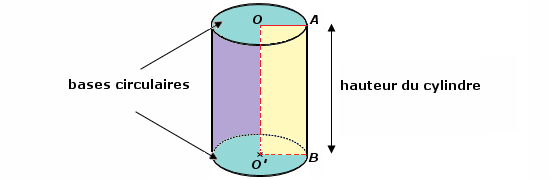
4.Le cylindre de révolution :

Définition :

Un cylindre de révolution est un solide composé d’une base qui est un disque dont les deux faces sont parallèles.

5.Patron d’un cylindre de révolution :

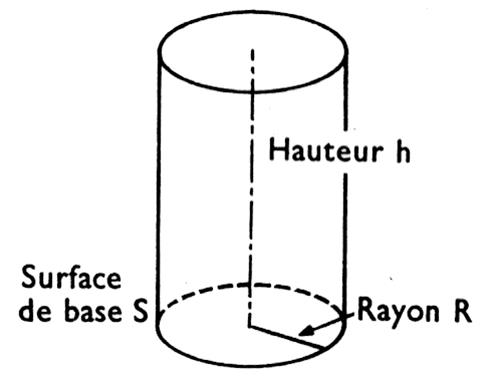
6.Volume d’un cylindre de révolution :

Propriété :

On considère un cylindre de révolution dont la base B est un disque de rayon R et de hauteur h.

Son volume est donné par la formule :

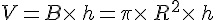
$V=B\times\,h=\pi\times\,R^2\times\,h$ .

Exemple :

Calculer le volume d’un cylindre dont la base est un disque de rayon 5 cm et de hauteur 7 cm.

Arrondir le résultat au centième.

$V=\pi\times\,R^2\times\,h\V=\pi\times\,5^2\times\,7\V=175\pi\V\approx\,549,78\,cm^3$

Le volume de ce cylindre est d’à peu près 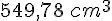$549,78\,cm^3$ .

II – Les solides avec une pointe :

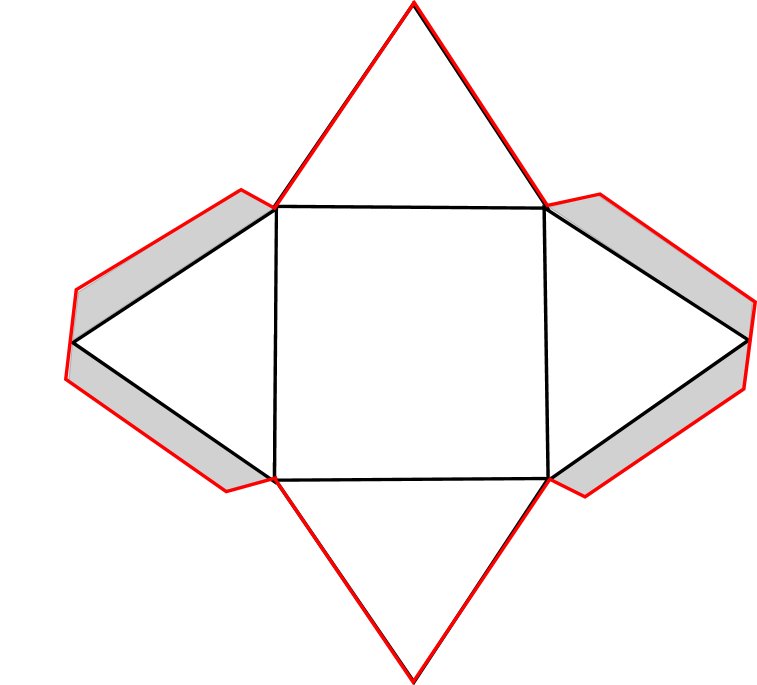
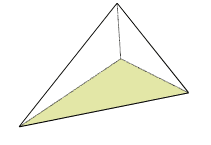
1.Les pyramides :

Définition :

Les pyramides ont pour base des polygones, et leurs faces latérales sont des triangles.

Patron d’une pyramide régulière à base carrée :

Propriété : volume d’une pyramide.

Soit une pyramide de base B et de hauteur h.

La formule de son volume est donnée par :

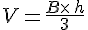
$V=\frac{B\times\,h}{3}$ .

Exemple :

Calculer le volume d’une pyramide dont la base est un carré de côté 5 cm et de hauteur 7,5 cm.

$V=\frac{B\times\,h}{3}=\frac{5\times\,5\times\,7,5}{3}=62,5\,cm^3$

Exemple :

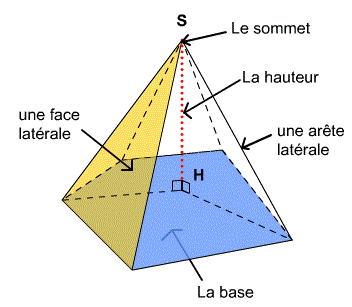
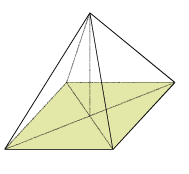
Le sommet de cette pyramide est le point S.
La base de cette pyramide est le pentagone ABCDE.
Les faces latérales sont les triangles SAB, SBC, SCD, SDE, SEA.
Les arêtes latérales sont les segments [AS], [BS], [CS], [DS], [ES].
La hauteur de la pyramide est le segment [OS].

remarques :

Une pyramide à base triangulaire s’appelle un tétraèdre.

Une pyramide régulière a une base qui est un polygone régulier ( par exemple un triangle équilatéral ou un carré) et dont les faces sont des triangles isocèles superposables. Sa hauteur passe par le centre de la base qui est le point de concours des diagonales.

Exemple :

Voici le patron d’une pyramide.

Sa base est un rectangle, de longueur 9 cm et de largeur 6 cm, et chaque arête latérale mesure 7 cm.

2.Les cônes de révolution :

Définition :

Les cônes de révolution ont pour base un disque.

Patron d’un cône de révolution :

Propriété : volume d’un cône de révolution.

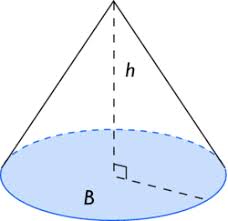
Soit un cône de révolution de base B, qui est un disque de rayon R, et de hauteur h.

La formule de son volume est donnée par :

$V=\frac{B\times\,h}{3}=\frac{\pi\times\,R^2\,\times\,h}{3}$ .

Exemple :

Calculer le volume d’un cône dont la base est un disque de rayon R= 3 cm et de hauteur 7,5 cm.

Arrondir le résultat au centième.

$V=\frac{B\times\,h}{3}\V=\frac{\pi\times\,R^2\,\times\,h}{3}\V=\frac{\pi\times\,3^2\,\times\,7,5}{3}\V=22,5\pi\V\approx\,70,69\,cm^3$

Exemple :

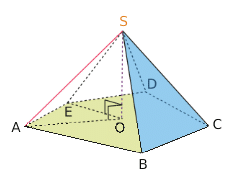
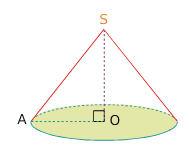
Le sommet du cône est le point S.
La base de ce cône est le disque de centre O : on la représente en perspective par un ovale ( une ellipse) car elle n’est pas vue de face.
La hauteur du cône est le segment [OS].
Le triangle AOS, rectangle en O, génère le cône tournant autour de (OS).
Une génératrice du cône est [SA].

Exemple :

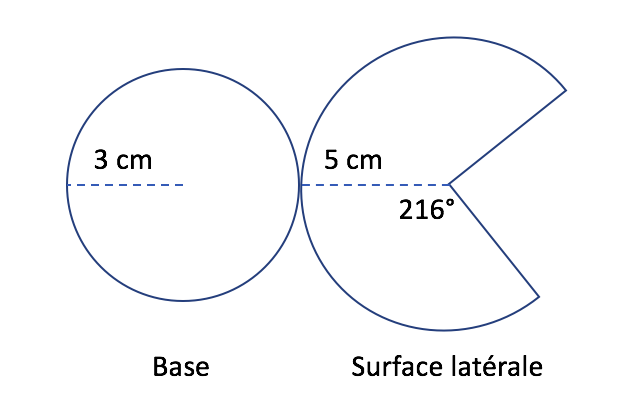
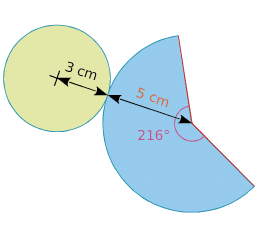
Voici le patron d’un cône de révolution de rayon de base 3 cm et de génératrice 5 cm.

La longueur du secteur de disque de rayon 5 cm est égales au périmètre de la base soit 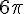$6\pi$ cm.

L’angle du secteur de disque est proportionnel à sa longueur. Il a pour angle $\frac{360\times\,6\pi}{10\pi}$ =36×6=216 °.

III. Calculs de volumes

Le cône de révolution et la pyramide sont des solides « pointus ».

Propriété :

Le volume est donné par la formule suivante :

Remarque :

Lorsque les longueurs sont exprimées en m, l’aire de la base est exprimée en m², et le volume en 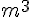m^3 .

Exemple :

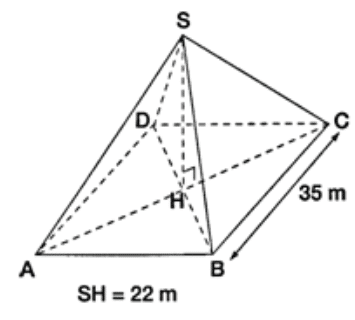
La pyramide du Louvre est une pyramide régulière à base carrée de 35 m de côté, sa hauteur est 22 m.
1. Calculer l’aire de sa base.
2. Calculer la valeur exacte du volume V de cette pyramide.
Donner la valeur arrondie de V au mètre cube.
3. Dans un parc de loisirs, on construit une réduction de cette pyramide ; le côté de la base carrée mesure 7 m.
a. Calculer l’échelle de cette réduction.
b. Calculer la hauteur de la pyramide réduite.
c. Par quel nombre faut-il multiplier le volume V de la pyramide du Louvre pour obtenir le volume V’ de la pyramide réduite ?

Exemple :

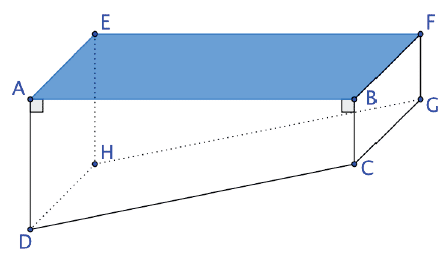
On donne: AB = 6 m, AE = 5 m, AD = 1,80 m, BC = 0,80 m .
Sur le schéma ci dessus, les dimensions ne sont pas respectées.
1. Montrer que le volume ce cette piscine est 39 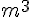m^3 .
2. A la fin de l’été, M. OBAMA vide sa piscine à l’aide d’une
pompe dont le débit est 5 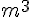m^3 par heure.

Calculer le nombre de 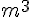m^3 restant dans la piscine au bout de 5 heures.

4.9/5 - (30074 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «pyramides, cônes et volumes de solides : cours de maths en 4ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Vous devez vous inscrire ou vous connecter à votre compte afin de pouvoir télécharger ce document au format PDF.

Cours de 4ème

Calcul littéral et double distributivité

Les équations et les problèmes

Fractions

Proportionnalité et vitesse moyenne

Exercices de 4ème

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

Scratch Heroes : escape game de programmation avec Scratch.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 552 035 cours et exercices de maths téléchargés en PDF et 4 250 exercices.