Statistiques avec médiane et moyenne : cours de maths en 3ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
Avant d’aborder cette leçon, il faut avoir acquis le contenu du cours sur les statistiques de l’année précédente.
I. L’étude Statistique :
Une enquête a été réalisée auprès des 450 élèves d’un collège.
Voici les questions posées :
- Comment viens-tu au collège ? A pied, en bus, en voiture ou à vélo ?
- Combien as-tu de frères et sœurs ?
- Quelle est la durée de ton trajet maison-collège ?
On a recueilli les données correspondant aux réponses des élèves : on obtient des séries statistiques
Les 450 élèves interrogés forment la population étudiée.
On considère une enquête statistiques.
L’ensemble auprès duquel l’enquête est menée est appelée la population.
Chaque élément de cette population a un effectif notés 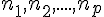
L’effectif total est la somme de tous ces effectifs (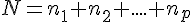
Le thème de l’enquête est appelé le caractère.
Le caractère peut être de deux sortes :
- quantitatif : si il est mesurable;
- qualitatif s’il n’est pas mesurable.
Exemple :
Demandons aux 27 élèves d’une classe de quatrième le nombre d’écrans qu’ils possèdent à la maison puis, la marque du véhicule de leurs parents.
La population : 27 élèves d’une classe de quatrième.
Caractère quantitatif : nombre d’écrans ( il est mesurable 0,1,2,etc…).
Caractère qualitatif : marque de véhicule (il est non mesurable Peugeot, Renault, Bmw, etc…).
Effectif total : N=27
II. La moyenne et la médiane d’une série statistiques :
On va étudier les différents caractères de cette population.
1.La fréquence d’une série statistiques :
La fréquence, notée f, d’une valeur est le quotient (ou rapport ) de l’effectif de cette valeur sur l’effectif total de la population.
La fréquence est en général donné en %, on la note f%.
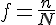
f % 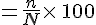
Exemple :
Considérons l’enquête menée sur le nombre de frères et soeurs.
C’est un caractère quantitatif.
0, 1, 2,…, 6 sont les valeurs de ce caractère.
La fréquence des élèves ayant 3 frères ou sœurs.
L’effectif est de 110 et l’effectif total est N = 450.
f %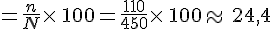
Globalement, nous obtenons :
2. La Moyenne pondérée et l’étendue d’une série statistiques :
Soit une série statistique telle que le caractère soit quantitatif.
Soient 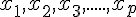
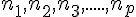
et N l’effectif total.
La moyenne de cette série statistiques, notée 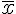
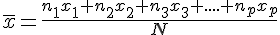
Pour calculer la moyenne pondérée d’une série de valeurs, il faut :
- calculer les produits de chaque valeur par leur coefficient (ou effectif),
- calculer la somme des produits.
- puis diviser le résultat par l’effectif total.
Exemple :
Reprenons l’exemple des frères et soeurs.
Calculons la moyenne de cette série statistiques.
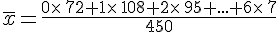
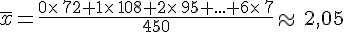
Exemple :
On a une suite de notes: 5; 12; 19; 12; 8; 10; 11; 14; 3; 8; 7; 12; 10; 9; 8; 16; 14; 8; 5; 11.
Calculer la moyenne de ces notes:
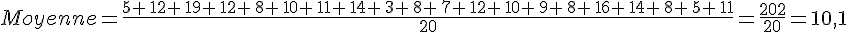
En reprenant la série de notes précédente, calculer les fréquences puis la moyenne de cette série statistiques.
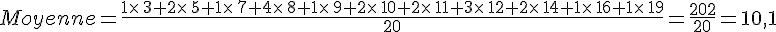
Signification concrète de la moyenne :
Si chaque élève devait obtenir la même note alors chaque élève obtiendrait 10,1 sur 20.
Une moyenne de 2,05 signifie que si chacun avait le même nombre de frères et soeurs
alors chacun aurait à peu près deux frères et soeurs.
L’étendue d’une série statistique est la différence entre la plus grande et la plus petite valeur prise par le caractère de la série.
Exemple
On a une suite de notes: 5; 12; 19; 12; 8; 10; 11; 14; 3; 8; 7; 12; 10; 9; 8; 16; 14; 8; 5; 11.
L’étendue des notes est de 19-3=16.
3. La médiane d’une série statistiques :
On appelle médiane d’une série statistique ordonnée une valeur du caractère qui partage la série en deux groupes de même effectif tels que :
- un groupe contient les valeurs inférieures ou égales à la médiane ;
- l’autre groupe contient les valeurs supérieures ou égales à la médiane.
Exemple 1 : cas d’un nombre impair de valeurs.
Voici les notes d’un groupe de 9 élèves lors d’un devoir de mathématiques.
5-6-11-13-6-14-12-8-13
Il faut d’abord ranger les nombres dans l’ordre croissant : 5-6-6-8-11-12-13-13-14
La médiane de cette série statistique est 11.
Exemple 2: cas d’un nombre pair de valeurs.
Voici les notes d’un groupe de 6 élèves lors d’un devoir de sciences physiques.
6-13-18-16-14-5
Il faut d’abord ranger les nombres dans l’ordre croissant : 5-6-13-14-16-18
La médiane de cette série statistique est la moyenne de la 3ème et 4ème valeur
donc 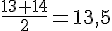
Signification concrète de la médiane :
Si la médiane du contrôle de sciences physiques est de 13,5 cela signifie qu’il y autant autant d’élèves qui ont eu une note inférieure à 13,5 que d’élèves qui ont eu une note supérieure à 13,5.
Télécharger ou imprimer cette fiche «statistiques avec médiane et moyenne : cours de maths en 3ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Exercices de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.















