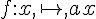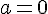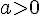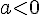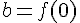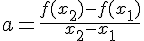Fonction linéaire et affine : cours de maths en 2de à imprimer en PDF.
Mis à jour le 29 mai 2025
A l’aide de ces différentes fonctions de références (linéaires, affines, carrées, inverse,…), nous allons pouvoir étudier de nombreuses autres fonctions numériques beaucoup plus complexes.
Cette leçon portera sur les notions d’images et d’antécédents ainsi que l’étude des courbes représentatives suivant les programmes officiels en vigueur de l’éducation nationale.
La fonction affine qui portera sur les notions d’images et d’antécédents ainsi que l’étude des courbes représentatives. L’élève devra connaître son expression algébrique qui est du type f(x)=ax+b où a est le coefficient directeur et b est l’ordonnée à l’origine. Cette leçon peut être imprimée ou téléchargée en PDF.
La fonction linéaire
I. Définition de la fonction linéaire.
Soit 
un nombre réel.
- On appelle fonction linéaire, toute fonction f définie par .
- Le nombre x est appelé l’antécédent du nombre f(x);
- Le nombre f(x) est appelé l’image de x par la fonction f.
II. Propriété de la courbe représentative.
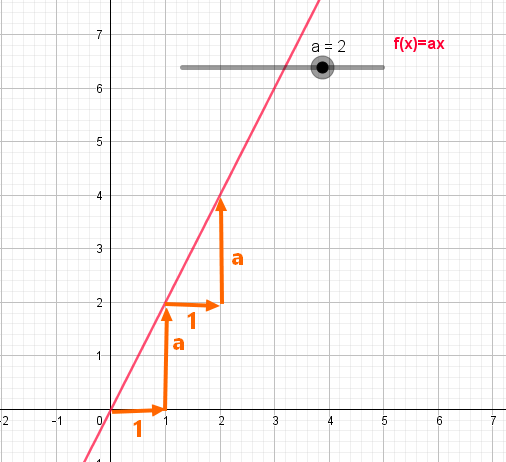
Dans un repère orthonormé du plan, la courbe d’une fonction linéaire est la droite d’équation y=ax passant par l’origine du repère.
Le nombre est appelé coefficient directeur de la droite.
III. Sens de variation d’une fonction linéaire.
Soit a un nombre réel et soit f la fonction linéaire telle que f(x)=ax pour tout nombre réel x.
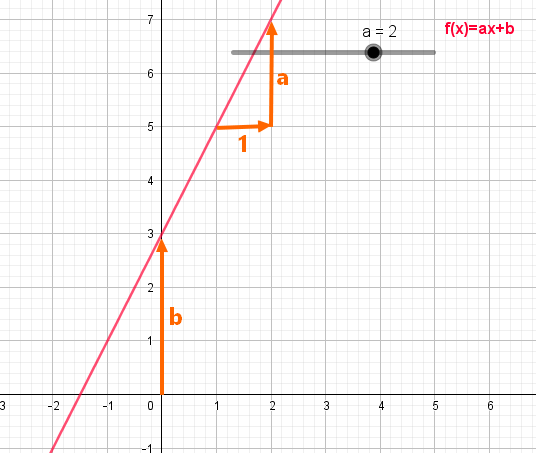
- Si alors f est la fonction nulle;
- Si alors la fonction f est croissante;
- Si alors la fonction f est décroissante.
Remarque :
- Si f est une fonction linéaire alors nous avons une situation de proportionnalité.
- Les grandeurs x et f(x) sont proportionnelles et le coefficient de proportionnalité correspond à la valeur du coefficient directeur.
- a=f(1)
La fonction affine
I. Définition de la fonction .
Soient et deux nombres réels.
On appelle fonction affine, toute fonction f définie par .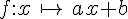
II. Propriétés de la fonction et vocabulaire.
Soit f une fonction affine telle que .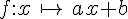
- Dans un repère orthonormé du plan, la courbe d’une fonction affine est la droite d’équation y=ax + b.
- Le nombre est appelé coefficient directeur de la droite.
- Le nombre est appelé l’ordonnée à l’origine.
Remarque :
Une fonction linéaire est une fonction affine mais la réciproque est fausse.
Contre-exemples :
est une fonction linéaire mais aussi affine car pour tout nombre réel x, nous avons .
est une fonction affine mais n’est pas linéaire.
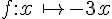
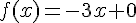
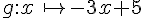
III. Sens de variation de la fonction.
Soit a et b deux nombres réels et soit f la fonction telle que f(x)=ax + b pour tout nombre réel x.
- Si alors f est une fonction constante;
- Si alors la fonction f est croissante;
- Si alors la fonction f est décroissante.
IV. Déterminer l’expression algébrique d’une fonction affine.
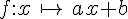
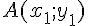
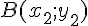
Soit f une fonction telle que .Soient et deux points distincts appartenant à la courbe de cette fonction.
Nous avons :
Télécharger ou imprimer cette fiche «fonction linéaire et affine : cours de maths en 2de à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Seconde
Exercices de Seconde
Nos applications
Téléchargez la dernière version gratuite de nos applications.
