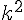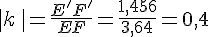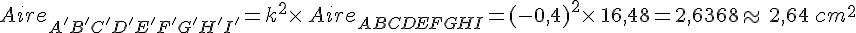Homothéties : cours de maths en 3ème en PDF.
Mis à jour le 20 décembre 2025
I. L’homothétie :
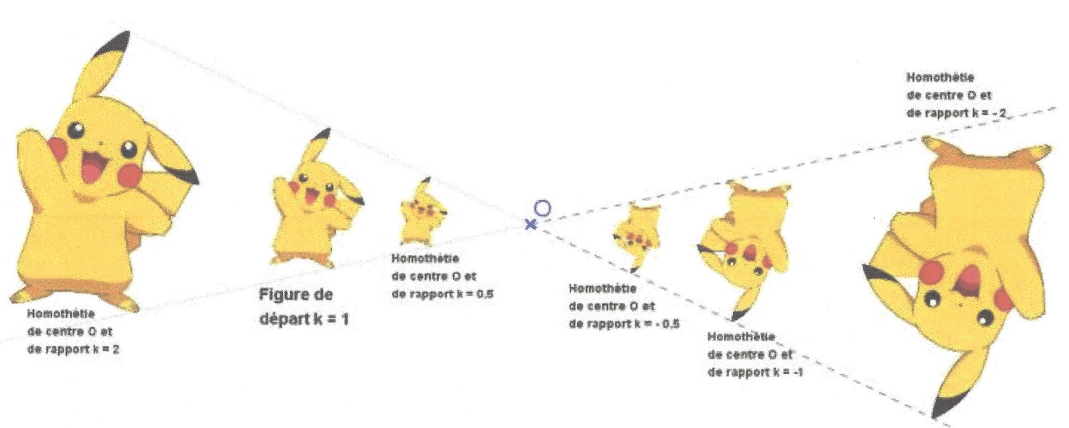
Transformer une figure par une homothétie de centre O, c’est l’agrandir ou la réduireen faisant glisser les points le long des droites passant par O.
L’image d’un point M par l’homothétie de centre O et de rapport k>0 est le point M’ tel que :
- M’ appartient à la demi-droite [OM);
Une homothétie conserve :
- l’alignement;
- la mesure des angles
- le parallélisme.
Si k >0, alors l’homothétie multiplie :
- les longueurs par k;
- les aires par
L’homothétie transforme une droite en une autre droite qui lui est parallèles.
Exemple :
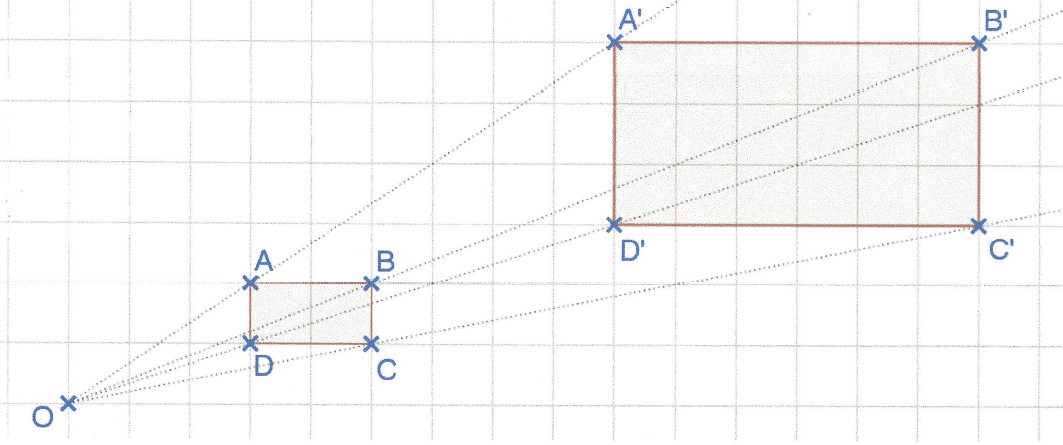
Le rectangle A’B’C’D’ est l’image du rectangle ABCD par l’homothétie de centre O et de rapport k=3.
AB = 2 cm donc 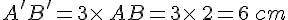
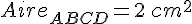
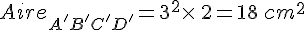
Application 1 :
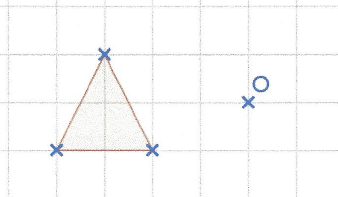
Construire les images du triangle par les homothéties de centre O et de rapport 3;-1 et – 2.
Remarque :
L’image du triangle de départ par l’homothétie de centre O et de rapport – 1 est en fait une symétrie centrale de centre O.
Application 2 :
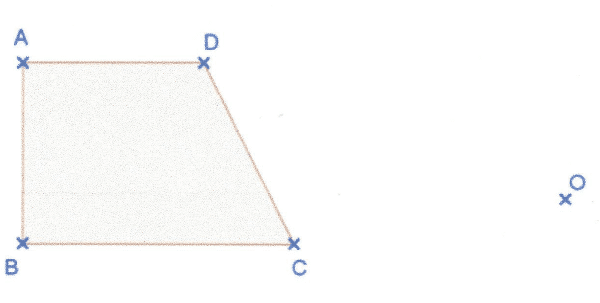
Construire les images du trapèze rectangle ABCD par les homothéties de centre O et de rapport 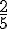
Application 3 :
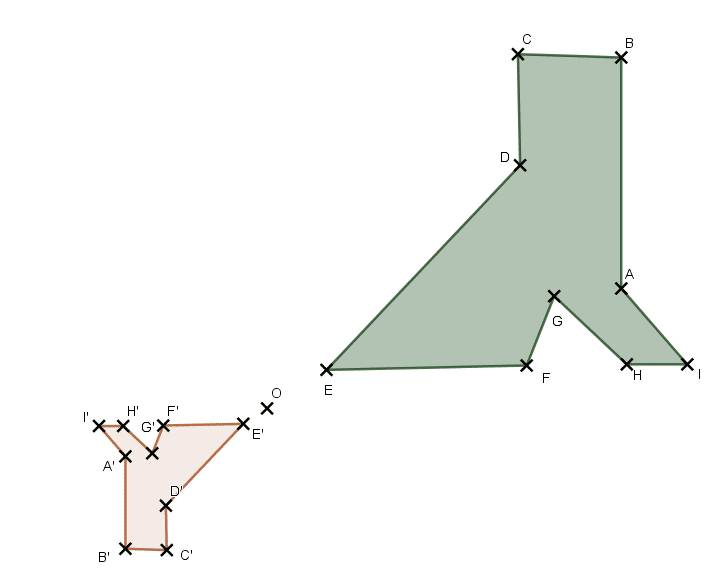
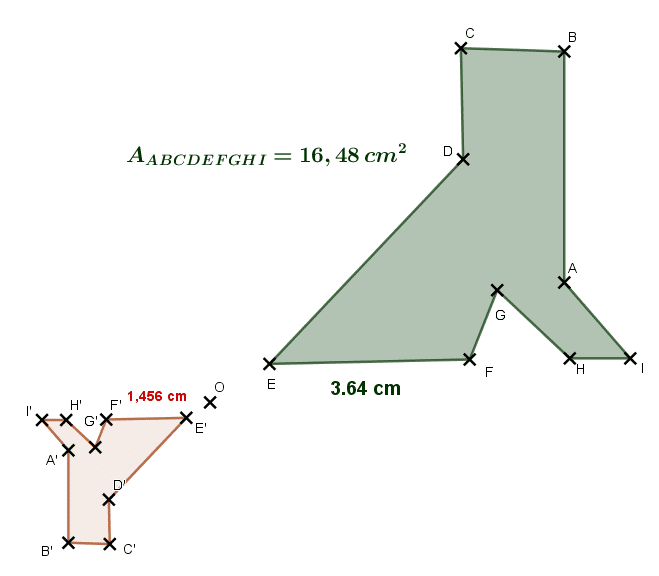
On considère l’homothétie de centre O et de rapport k qui transforme la chaussure verte en la chaussure rouge.
- Est-ce un agrandissement ou une réduction ? justifier votre réponse.
- Quel est la valeur du rapport k?
- Calculer l’aire de la chaussure rouge (arrondir le résultat au centième).
Solution :
- C’est un agrandissement car nous observons que EF = 3,64 cm et E’F’ = 1,46 cm.
Télécharger ou imprimer cette fiche «homothéties : cours de maths en 3ème en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 3ème
Exercices de 3ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.