L’addition : corrigés des exercices de maths en 6ème.

Exercice 1 : poser une addition
a. $14%2C57\,%2B\,8%2C6$
$14%2C57\,%2B\,8%2C6\,=\,14%2C57\,%2B\,8%2C60\,=\,23%2C17$

b. $214%2C12\,%2B\,7%2C48$
$214%2C12\,%2B\,7%2C48\,=\,221%2C60$

c. $35%2C58\,%2B\,28%2C73$
$35%2C58\,%2B\,28%2C73\,=\,64%2C31$

d. $29%2C17\,%2B\,3%2C554$
$29%2C17\,%2B\,3%2C554\,=\,29%2C170\,%2B\,3%2C554\,=\,32%2C724$

Exercice 2 : ordre de grandeur d’une addition

1) $27%2C28\,%2B\,187%2C49$

$27%2C28\,\approx\,30$ et $187%2C49\,\approx\,190$

Donc, $27%2C28\,%2B\,187%2C49\,\approx\,30\,%2B\,190\,=\,\mathbf{220}$ .

2) $152%2C03\,%2B\,490%2C75$

$152%2C03\,\approx\,150$ et $490%2C75\,\approx\,490$

Donc, $152%2C03\,%2B\,490%2C75\,\approx\,150\,%2B\,490\,=\,\mathbf{640}$ .

3) $2\%2C543%2C37\,%2B\,3\%2C482%2C25$

$2\%2C543%2C37\,\approx\,2\%2C540$ et $3\%2C482%2C25\,\approx\,3\%2C480$

Donc, $2\%2C543%2C37\,%2B\,3\%2C482%2C25\,\approx\,2\%2C540\,%2B\,3\%2C480\,=\,\mathbf{6\%2C020}$ .

4) $3\%2C742%2C18\,%2B\,623%2C132$

$3\%2C742%2C18\,\approx\,3\%2C740$ et $623%2C132\,\approx\,620$

Donc, $3\%2C742%2C18\,%2B\,623%2C132\,\approx\,3\%2C740\,%2B\,620\,=\,\mathbf{4\%2C360}$ .

Exercice 3 : trouver l’erreur
a. Évariste:

Erreur:
Évariste a mal additionné des chiffres. Le calcul correct est le suivant:

Posons l’addition correctement:

$47%2C3\,%2B5%2C48=52%2C72$

b. Allan:

Erreur:
Allan a aussi commis une erreur en additionnant les chiffres. Le calcul correct est le suivant:

Posons l’addition correctement:

$7%2C9\,%2B\,63%2C48\,=\,71%2C38$

Conclusion: Allan n’a pas pris en compte correctement toutes les retenues intermédiaires.

Exercice 4 : poser et effectuer les additions
$\begin{array}{rl}%0D%0A1.\,%26\,53\,%2B\,42\,=\,95\,\\%0D%0A2.\,%26\,512\,%2B\,395\,=\,907\,\\%0D%0A3.\,%26\,987\,%2B\,47\,=\,1\%2C034\,\\%0D%0A4.\,%26\,6\%2C528\,%2B\,2\%2C410\,=\,8\%2C938\,\\%0D%0A5.\,%26\,56\%2C812\,%2B\,9\%2C874\,=\,66\%2C686\,\\%0D%0A6.\,%26\,1\%2C523\,%2B\,250\,%2B\,45\,=\,1\%2C818\,\\%0D%0A7.\,%26\,651\%2C232\,%2B\,289\%2C002\,=\,940\%2C234\,\\%0D%0A8.\,%26\,862\%2C231\,%2B\,51\%2C236\,%2B\,521\,=\,914\%2C048\,\\%0D%0A\end{array}$

Exercice 6 : calculer des sommes

[a.]
$6%2C5\,%2B\,12%2C6\,%2B\,1%2C5\,=\,(6%2C5\,%2B\,1%2C5)\,%2B\,12%2C6\,=\,8\,%2B\,12%2C6\,=\,20%2C6$

[b.]
$36%2C99\,%2B\,45%2C74\,%2B\,2%2C01\,%2B\,13%2C26\,=\,(36%2C99\,%2B\,2%2C01)\,%2B\,(45%2C74\,%2B\,13%2C26)\,=\,39\,%2B\,59\,=\,98$

[c.]
$9%2C25\,%2B\,8%2C7\,%2B\,5%2C3\,%2B\,16%2C75\,=\,(9%2C25\,%2B\,5%2C3)\,%2B\,(8%2C7\,%2B\,16%2C75)\,=\,14%2C55\,%2B\,25%2C45\,=\,40$

[d.]
$34%2C645\,%2B\,34%2C75\,%2B\,2%2C25\,%2B\,4%2C355\,=\,(34%2C645\,%2B\,4%2C355)\,%2B\,(34%2C75\,%2B\,2%2C25)\,=\,39\,%2B\,37\,=\,76$

[e.]
$7%2C42\,%2B\,4%2C2\,%2B\,7%2C8\,%2B\,25%2C58\,=\,(7%2C42\,%2B\,7%2C8)\,%2B\,(4%2C2\,%2B\,25%2C58)\,=\,15%2C22\,%2B\,29%2C78\,=\,45$

[f.]
$3%2C01\,%2B\,2%2C9\,%2B\,6%2C1\,%2B\,7%2C99\,%2B\,2%2C001\,=\,(3%2C01\,%2B\,6%2C1)\,%2B\,(2%2C9\,%2B\,7%2C99)\,%2B\,2%2C001\,=\,9%2C11\,%2B\,10%2C89\,%2B\,2%2C001\,=\,22%2C001$

Exercice 7 : calculer des sommes astucieusement
1/ $8%2C\,17\,%2B\,6%2C\,7\,%2B\,6%2C\,83\,%2B\,3%2C\,3$

$=\,8%2C\,23%2C\,13%2C\,86%2C\,3$

En regroupant astucieusement :
$8\,%2B\,3\,%2B\,23\,%2B\,13\,%2B\,86\,=\,133$

2/ $3%2C\,4\,%2B\,0%2C\,88\,%2B\,1%2C\,6\,%2B\,0%2C\,12$

$=\,3%2C\,4%2C\,89%2C\,6%2C\,12$

En regroupant astucieusement :
$3\,%2B\,4\,%2B\,89\,%2B\,6\,%2B\,12\,=\,114$

3/ $6%2C\,8\,%2B\,5%2C\,7\,%2B\,4%2C\,3\,%2B\,3%2C\,2$

$=\,6%2C\,13%2C\,11%2C\,6%2C\,2$

En regroupant astucieusement :
$6\,%2B\,6\,%2B\,2\,%2B\,13\,%2B\,11\,=\,38$

4/ $12%2C\,1\,%2B\,12%2C\,4\,%2B\,12%2C\,9\,%2B\,12%2C\,6$

$=\,12%2C\,13%2C\,16%2C\,21%2C\,6$

En regroupant astucieusement :
$12\,%2B\,13\,%2B\,16\,%2B\,21\,%2B\,6\,=\,68$

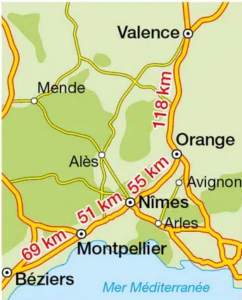
Exercice 8 : problème sur les additions

a. Distance entre Valence et Nîmes :
$118\%2C\,km$

b. Distance entre Béziers et Nîmes :
$69\%2C\,km$

c. Distance entre Valence et Béziers :
$118\%2C\,km\,%2B\,55\%2C\,km\,%2B\,51\%2C\,km\,%2B\,69\%2C\,km\,=\,293\%2C\,km$

Exercice 9 : calculer les sommes suivantes
$\begin{array}{cccccc}%0D%0A\phantom{00}\,1\,%26\,2\,%26\,3\,%26\,\phantom{00}\,%26\,2\,%26\,5\,%26\,6\,%26\,3\,%26\,\phantom{00}\,%26\,8\,%26\,2\,\\%0D%0A%2B\,%26\,5\,%26\,6\,%26\,4\,%26\,%2B\,%26\,3\,%26\,2\,%26\,1\,%26\,%2B\,%26\,1\,%26\,1\,%26\,1\,%26\,\\%0D%0A\hline%0D%0A\phantom{00}\,6\,%26\,8\,%26\,7\,%26\,\phantom{00}\,%26\,2\,%26\,8\,%26\,8\,%26\,4\,%26\,\phantom{00}\,%26\,9\,%26\,3\,%26\,\phantom{00}\,\\%0D%0A\end{array}$

$\begin{array}{cccccc}%0D%0A\phantom{00}\,8\,%26\,2\,%26\,9\,%26\,\phantom{00}\,%26\,3\,%26\,5\,%26\,7\,%26\,5\,%26\,\phantom{00}\,%26\,3\,%26\,2\,\\%0D%0A%2B\,%26\,5\,%26\,6\,%26\,2\,%26\,%2B\,%26\,8\,%26\,2\,%26\,6\,%26\,%2B\,%26\,1\,%26\,7\,%26\,5\,%26\,\\%0D%0A\hline%0D%0A\phantom{00}\,1\,%26\,3\,%26\,9\,%26\,1\,%26\,\phantom{00}\,%26\,4\,%26\,4\,%26\,0\,%26\,1\,%26\,\phantom{00}\,%26\,2\,%26\,0\,%26\,7\,\\%0D%0A\end{array}%0D%0A\vspace{10mm}$

$\begin{array}{cccc}%0D%0A\phantom{00}\,3\,%26\,2\,%26\,\phantom{00}\,\quad%2B\,9\,%26\,1\,%26\,3\,%26\,\phantom{00}\,\\%0D%0A%2B\,%26\,1\,%26\,7\,%26\,5\,%26\,\\%0D%0A\hline%0D%0A5\,%26\,8\,%26\,\phantom{00}\,\quad%2B\,1\,%26\,1\,%26\,9\,%26\,\phantom{00}\,\\%0D%0A\end{array}$

Exercice 10 : calculer de tête ces additions
a. $37\,%2B\,9\,=\,46$

b. $48\,%2B\,98\,=\,146$

c. $125\,%2B\,99\,=\,224$

d. $2136\,-\,999\,=\,1137$

e. $107\,%2B\,49\,=\,156$

f. $34\,%2B\,28\,=\,62$

g. $105\,-\,38\,=\,67$

h. $48\,-\,9\,=\,39$

i. $277\,%2B\,998\,=\,1275$

j. $125\,-\,18\,=\,107$

k. $63\,%2B\,39\,=\,102$

l. $300\,-\,78\,=\,222$

Exercice 11 : donner un ordre de grandeur

[a.] $108\,%2B\,295\,\approx\,100\,%2B\,300$

$108\,%2B\,295\,\approx\,400$

[b.] $839\,-\,42\,\approx\,840\,-\,40$

$839\,-\,42\,\approx\,800$

[c.] $439\,-\,177\,\approx\,440\,-\,180$

$439\,-\,177\,\approx\,260$

[d.] $5\%2C365\,%2B\,2\%2C841\,%2B\,11\%2C723\,\approx\,5\%2C000\,%2B\,3\%2C000\,%2B\,12\%2C000$

$5\%2C365\,%2B\,2\%2C841\,%2B\,11\%2C723\,\approx\,20\%2C000$

[e.] $16\%2C432.78\,-\,5\%2C645.999\,\approx\,16\%2C000\,-\,6\%2C000$

$16\%2C432.78\,-\,5\%2C645.999\,\approx\,10\%2C000$

[f.] $651\%2C248\,%2B\,17\,%2B\,328\%2C421\,\approx\,650\%2C000\,%2B\,0\,%2B\,330\%2C000$

$651\%2C248\,%2B\,17\,%2B\,328\%2C421\,\approx\,980\%2C000$

[g.] $0.58\,%2B\,1.32\,%2B\,0.175\,\approx\,0.6\,%2B\,1.3\,%2B\,0.2$

$0.58\,%2B\,1.32\,%2B\,0.175\,\approx\,2.1$

Exercice 12 : carré avec sommes égales
a.
$\begin{array}{%7Cc%7Cc%7Cc%7C}%0D%0A\hline%0D%0A6\,%26\,8\,%26\,14\,\\%0D%0A\hline%0D%0A15\,%26\,10\,%26\,3\,\\%0D%0A\hline%0D%0A12\,%26\,6\,%26\,10\,\\%0D%0A\hline%0D%0A\end{array}$

b.
$\begin{array}{%7Cc%7Cc%7Cc%7C}%0D%0A\hline%0D%0A7%2C5\,%26\,2%2C5\,%26\,2\,\\%0D%0A\hline%0D%0A2%2C5\,%26\,4%2C5\,%26\,5\,\\%0D%0A\hline%0D%0A3%2C5\,%26\,1%2C5\,%26\,7\,\\%0D%0A\hline%0D%0A\end{array}$

c.
$\begin{array}{%7Cc%7Cc%7Cc%7C}%0D%0A\hline%0D%0A1%2C6\,%26\,1%2C3\,%26\,0%2C6\,\\%0D%0A\hline%0D%0A0%2C9\,%26\,1%2C1\,%26\,1%2C5\,\\%0D%0A\hline%0D%0A0%2C4\,%26\,1%2C4\,%26\,2%2C1\,\\%0D%0A\hline%0D%0A\end{array}$

Exercice 13 : calculer avec des regroupements astucieux
a. $A\,=\,8%2C5\,%2B\,12%2C7\,%2B\,1%2C5$
En regroupant 8,5 et 1,5 :
$A\,=\,(8%2C5\,%2B\,1%2C5)\,%2B\,12%2C7%0D%0A=\,10\,%2B\,12%2C7%0D%0A=\,22%2C7$

b. $B\,=\,18%2C3\,%2B\,1%2C7\,%2B\,6%2C8$
En regroupant 18,3 et 1,7 :
$B\,=\,(18%2C3\,%2B\,1%2C7)\,%2B\,6%2C8%0D%0A=\,20\,%2B\,6%2C8%0D%0A=\,26%2C8$

c. $C\,=\,3%2C6\,%2B\,7\,%2B\,11%2C4$
En regroupant 3,6 et 11,4 :
$C\,=\,(3%2C6\,%2B\,11%2C4)\,%2B\,7%0D%0A=\,15\,%2B\,7%0D%0A=\,22$

Exercice 14 : calculer les sommes et les différences
$\begin{array}{cccc}%0D%0A12%2C3\,%26\,84%2C25\,%26\,3%2C57\,%26\,\\%0D%0A%2B\,5%2C4\,%26\,%2B\,32%2C18\,%26\,%2B\,82%2C6\,%26\,\\%0D%0A\hline%0D%0A17%2C7\,%26\,116%2C43\,%26\,86%2C17\,%26\,\\%0D%0A\end{array}$

$\begin{array}{cccc}%0D%0A0%2C839\,%26\,51%2C62\,%26\,32%2C094\,%26\,\\%0D%0A%2B\,5%2C362\,%26\,%2B\,15%2C21\,%26\,%2B\,17%2C19\,%26\,\\%0D%0A\hline%0D%0A6%2C201\,%26\,66%2C83\,%26\,49%2C284\,%26\,\\%0D%0A\end{array}$

$\begin{array}{c}%0D%0A51%2C62\,\\%0D%0A%2B\,15%2C21\,\\%0D%0A%2B\,7%2C195\,\\%0D%0A\hline%0D%0A74%2C025\,\\%0D%0A\end{array}$

$\begin{array}{c}%0D%0A125%2C8\,\\%0D%0A-\,45%2C6\,\\%0D%0A\hline%0D%0A80%2C2\,\\%0D%0A\end{array}$

$\begin{array}{c}%0D%0A90\,\\%0D%0A-\,52%2C3\,\\%0D%0A\hline%0D%0A37%2C7\,\\%0D%0A\end{array}$

$\begin{array}{c}%0D%0A10%2C2\,\\%0D%0A-\,7%2C54\,\\%0D%0A\hline%0D%0A2%2C66\,\\%0D%0A\end{array}$

$\begin{array}{c}%0D%0A4%2C8\,\\%0D%0A-\,3%2C178\,\\%0D%0A\hline%0D%0A1%2C622\,\\%0D%0A\end{array}$

$\begin{array}{c}%0D%0A4%2C09\,\\%0D%0A-\,0%2C87\,\\%0D%0A\hline%0D%0A3%2C22\,\\%0D%0A\end{array}$

$\begin{array}{c}%0D%0A47%2C53\,\\%0D%0A-\,37%2C72\,\\%0D%0A\hline%0D%0A9%2C81\,\\%0D%0A\end{array}$

Exercice 15 : calculer les additions en regroupant astucieusement
a. $25\,%2B\,128\,%2B\,175\,%2B\,22$

Regroupement astucieux :
$(25\,%2B\,175)\,%2B\,(128\,%2B\,22)$
$200\,%2B\,150\,=\,350$

b. $357\,%2B\,149\,%2B\,43\,%2B\,51$

Regroupement astucieux :
$(357\,%2B\,43)\,%2B\,(149\,%2B\,51)$
$400\,%2B\,200\,=\,600$

c. $2%2C45\,%2B\,3%2C8\,%2B\,1%2C55\,%2B\,14%2C2$

Regroupement astucieux :
$(2%2C45\,%2B\,1%2C55)\,%2B\,(3%2C8\,%2B\,14%2C2)$
$4\,%2B\,18\,=\,22$

d. $7%2C48\,%2B\,1%2C03\,%2B\,4%2C52\,%2B\,3%2C47$

Regroupement astucieux :
$(7%2C48\,%2B\,4%2C52)\,%2B\,(1%2C03\,%2B\,3%2C47)$
$12\,%2B\,4%2C5\,=\,16%2C5$

Exercice 16 : ces deux élèves ont commis une erreur

a. Évariste:

Erreur:
Évariste a mal additionné des chiffres. Le calcul correct est le suivant:

Posons l’addition correctement:

$47%2C3\,%2B5%2C48=52%2C72$

b. Allan:

Erreur:
Allan a aussi commis une erreur en additionnant les chiffres. Le calcul correct est le suivant:

Posons l’addition correctement:

$7%2C9\,%2B\,63%2C48\,=\,71%2C38$

Conclusion: Allan n’a pas pris en compte correctement toutes les retenues intermédiaires.

Exercice 17 : poser l’addition puis vérifier à la calculatrice

a. 14,57 + 8,6

$14%2C57\,%2B\,8%2C6\,\,=\,14%2C57\,%2B\,8%2C60\,=\,23%2C17$
b. 214,12 + 7,48

$214%2C12\,%2B\,7%2C48=\,221%2C60$
c. 35,58 + 28,73

$35%2C58\,%2B\,28%2C73=\,64%2C31$
d. 29,17 + 3,554

$29%2C17\,%2B\,3%2C554\,=\,32%2C724$
Exercice 18 : le prix du baril de pétrole
Soit le prix du baril de pétrole cinq mois avant décembre 2015.

Début décembre 2015, le prix était de 40,97 $. On sait également que cinq mois avant, le prix était supérieur de 16,89 $.

Ainsi, on peut écrire l’équation suivante :
$P\,=\,40%2C97\,%2B\,16%2C89$

Calculons :
$P\,=\,40%2C97\,%2B\,16%2C89\,=\,57%2C86$

Donc, le prix du baril de pétrole cinq mois avant décembre 2015 était de 57,86 $.

Exercice 19 : la hauteur d’un iceberg
a. Donner un ordre de grandeur de la hauteur de la partie immergée.

L’ordre de grandeur de la partie immergée peut être estimé en sachant que la majeure partie d’un iceberg est généralement sous l’eau. Environ 90% d’un iceberg est immergé.

$Hauteur\,immergee\,\approx\,0.9\,\times \,hauteur\,totale$