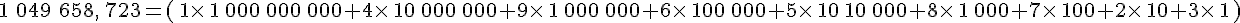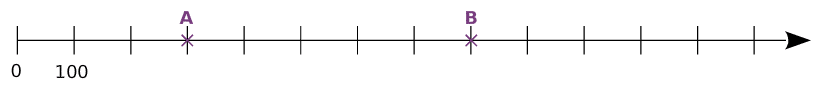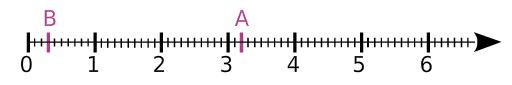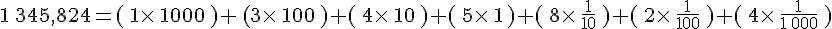Nombres décimaux : cours de maths en 6ème à imprimer en PDF.

Mis à jour le 14 juillet 2025

Sommaire

📚Cours de Mathématiques6ème • collège

Nombres décimaux

⏱️Temps de lecture : 9 min

🎯Difficulté : Initiation

📚Cycle 3

📋Prérequis : Programme CM2 maîtrisé

📄Format PDF disponible gratuitement

Les nombres décimaux avec un cours de maths en 6ème, nous aborderons le vocabulaire et la définition d’un nombre décimal, ainsi que les différentes décomposition d’un nombre décimal. Nous terminerons cette leçon avec le positionnement sur une droite graduée puis, la comparaison de nombres décimaux. Cette leçon reprend toutes les notions du programme officiel de l’éducation nationale en maths et permet aux élèves d’assimiler le contenu de leur leçon.

Vous retrouverez toutes les définitions, les propriétés et les théorèmes que vous abordez en classe avec votre professeur ou dans votre manuel scolaire (Nathan, Hatier, Sésamaths).

L’élève doit être capable de comparer deux nombres entiers mais également, de pouvoir les ranger dans l’ordre croissant ou décroissant.

Nous aborderons les nombres entiers ainsi que la position d’un chiffre puis, l’ordre croissant et décroissant ainsi que la comparaison de deux nombres entiers en clase de sixième.

I. Décomposition et nom des chiffres

Règle :

En mathématiques, nous disposons de dix chiffres 0,1,2,3,4,5,6,7,8,9 qui permettent d’écrire tous les nombres entiers, de même que les 26 lettres de l’alphabet de A à Z permettent d’écrire tous les mots.

Exemple :

1 054 est un nombre de quatre chiffres;
7 est un nombre d’un seul chiffre.

Règle :

Pour pouvoir lire les grands nombres entiers facilement, on regroupe les chiffres

par tranche de trois, en partant de la droite.

Exemple :

1049658723 s’écrit 1 049 658 723

a. Ce nombre s’écrit un-milliard-quarante-neuf-million-six-cent-cinquante-huit-mille-sept-cent-vingt-trois.
Il se décompose comme ci-contre : $1\,\,049\,\,658,\,723=,(\,1\times \,1\,000\,000\,000+4\times \,10\,000\,000+9\times \,1\,000\,000+6\times \,100\,000+5\times \,10\,10\,000+8\times \,1\,000+7\times \,100+2\times \,10+3\times \,1\,\,)$
7 est le chiffre des centaines et 4 est le chiffre des dizaines de millions.
Le nombre de millions est 1 049. A ne pas confondre avec le chiffre des millions qui est 9.

II. Sous-multiples de l’unité

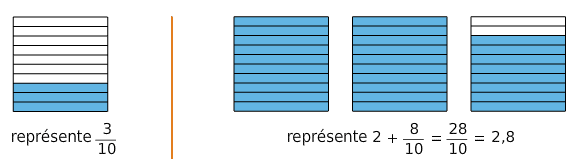
1.Les dixièmes

Définition :

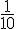
Lorsque l’on décompose une unité en dix parties égales, on obtient des dixièmes.Un dixième se note $\frac{1}{10}$ .

Dans l’unité, il y a dix dixièmes donc 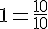$1=\frac{10}{10}$ .

Exemple :

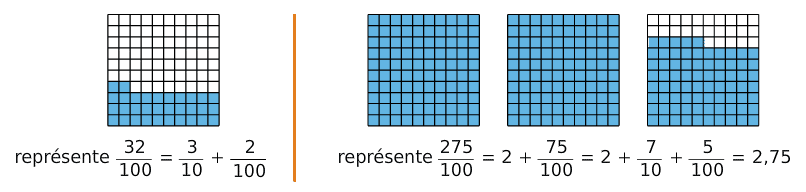
2. Les centièmes

Définition :

Lorsque l’on décompose une unité en cent parties égales, on obtient un centième.Un centième se note 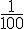$\frac{1}{100}$ .

Dans l’unité, il y a cent centièmes donc 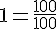$1=\frac{100}{100}$ .

Exemple :

3.Les millièmes

Définition :

Lorsque l’on décompose une unité en mille parties égales, on obtient des millièmes.Un millième se note 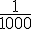$\frac{1}{1000}$ .

Dans l’unité il y a mille millième donc 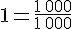$1=\frac{1\,000}{1\,000}$ .

Exemple :

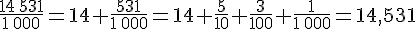
$\frac{14\,531}{1\,000}=14+\frac{531}{1\,000}=14+\frac{5}{10}+\frac{3}{100}+\frac{1}{1\,000}=14,531$

III. Définitions et vocabulaire sur les nombres décimaux :

Définition :

Lorsque l’on partage l’unité en dix parties égales, nous obtenons un dixième de l’unité.
Lorsque l’on partage chaque dixième en dix parties égales, nous obtenons un centième de l’unité.
En continuant ce procédé de partage, nous obtenons des millièmes, des dix-millièmes ….

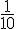
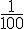
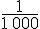
Un dixième se note $\frac{1}{10}$ , un centième se note $\frac{1}{100}$ , un millième se note $\frac{1}{1\,000}$ .

Nous avons 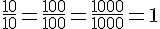$\frac{10}{10}=\frac{100}{100}=\frac{1000}{1000}=1$ .

Définition :

Une fraction dont le dénominateur ou/et le numérateur sont des nombres décimaux non nuls est appelée écriture fractionnaire.
Une fraction dont le dénominateur est 1,10, 100, 1 000 etc… est appelée fraction décimale.
Un nombre décimal est un nombre qui peut s’écrire sous la forme d’une fraction décimale.

Exemples :

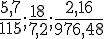
$\frac{5,7}{115};\frac{18}{7,2};\frac{2,16}{976,48}$ sont des écriture fractionnaires.

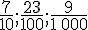
$\frac{7}{10};\frac{23}{100};\frac{9}{1\,000}$ sont des fractions décimales.

Le nombre 7,214 est bien un nombre décimal puisque 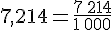$7,214=\frac{7\,214}{1\,000}$ .

Le nombre 0,002 59 est bien un nombre décimal puisque 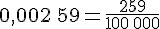$0,002\,59=\frac{259}{100\,000}$ .

Le nombre 1,333333……. n’est pas un nombre décimal car il ne peut pas s’écrire sous forme d’une fraction décimal.

Remarque :

Tout nombre entier est un nombre décimal.

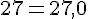
27=27,0

Propriété :

Tout nombre décimal peut s’écrire comme la somme d’un nombre entier (qui représente sa partie entière) et d’une fraction décimale inférieure à 1 (qui représente sa partie décimale).On peut également utiliser une virgule pour fournir son écriture décimale.

Exemples :

$37,2=37+\frac{2}{10}$

$948,736=948+\frac{7}{10}+\frac{3}{100}+\frac{6}{1\,000}$

Propriété :

Tout nombre décimal possède une infinité de décompositions décimales.

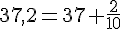
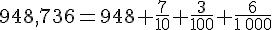
Exemples :

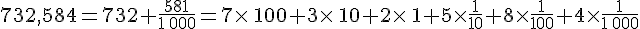
$732,584=732+\frac{581}{1\,000}=7\times \,100+3\times \,10+2\times \,1+5\times \frac{1}{10}+8\times \frac{1}{100}+4\times \frac{1}{1\,000}$

ou encore 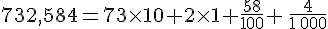$732,584=73\times 10+2\times 1+\frac{58}{100}+\,\frac{4}{1\,000}$ etc….

IV. Positionnement et écriture d’un nombre décimal :

Propriété :

Dans une écriture décimale, la valeur d’un chiffre dépend de sa position dans le nombre.

Exemple :

Prenons le nombre décimal 732,584.

2 est le chiffre des unités;
3 est le chiffre des dizaines;
7 est le chiffre des centaines;
5 est le chiffre des dixièmes;
8 est le chiffre des centièmes;
4 est le chiffre des millièmes;
Il y a 73 dizaines, il y a 7 325 dixièmes, il y a 73 258 centièmes, il y a 732 584 millièmes.

V. Repérage sur une demi-droite graduée et nombres décimaux :

Définition :

Une demi-droite graduée est une demi-droite sur laquelle on a reporté régulièrementune unité de longueur à partir de son origine le point O.

Propriété :

Sur une demi-droite graduée, un point est repéré par un nombre unique appelé son abscisse de ce point.L’origine du repère notée O, a pour abscisse 0.

Exemple :

Donner les abscisses des points A et B.

Le point A a pour abscisse 300. On note A(300).
Le point B a pour abscisse 800. On note B(800).

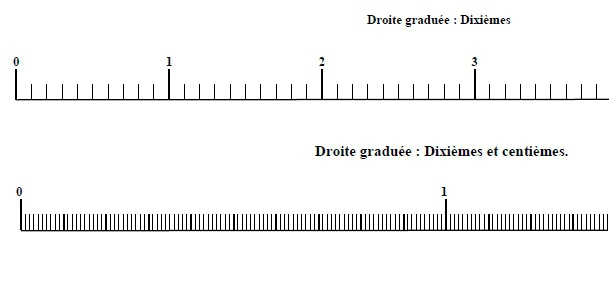
Exemple :

Quelles sont les abscisses des points A et B?

Une unité est divisée en dix parts égales, ce qui signifie qu’elle est partagée en dix-dixièmes.

Le point A se trouve 2 dixièmes après 3. Donc son abscisse est 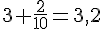$3+\frac{2}{10}=3,2$ .

Le point B a pour abscisse 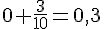$0+\frac{3}{10}=0,3$ .

On note A(3,2) et B(0,3).

Définition :

Une demi-droite graduée est une demi-droite sur laquelle nous avons choisi une unité de longueur, que l’on a reporté régulièrement à partir du point origine noté O.
Tout nombre décimal peut être représenté par un point sur une droite graduée. Ce nombre est appelé l’abscisse du point.

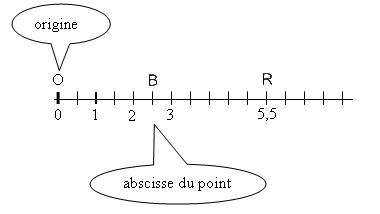
Exemple :

Dans l’exemple ci-dessus, le point B a pour abscisse 2,5 et nous notons B(2,5).

VI. Comparaison et rangement

1.Comparaison de deux nombres décimaux

Définition :

Comparer deux nombres, c’est trouver qui est le plus grand, ou le plus petit, ou dire si ils sont égaux.

Remarque :

On utilise les symboles > pour « plus grand que » et < pour « plus petit que ».

Règle :

Pour comparer deux nombres décimaux écrits sous forme décimale :

on compare les parties entières;
si les parties entières sont égales, alors on compare les chiffres de dixièmes;
ils sont égaux, donc on compare les chiffres des centièmes;
ils sont égaux, donc on compare les chiffres des millièmes;
et ainsi de suite jusqu’à ce que les deux nombres aient des chiffres différents.

Exemple :

Comparer les nombres 81,357 et 81,36.

On compare d’abord les parties entières des deux nombres;
elles sont égales, donc on compare les chiffres des dixièmes;
ils sont égaux, donc on compare les chiffres des centièmes.
5<6 donc 81,357<81,36.

Remarque :

Quand les parties entières sont égales, on peut comparer les parties décimales.

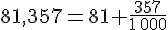
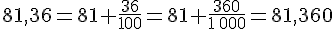
$81,357=81+\frac{357}{1\,000}$ et $81,36=81+\frac{36}{100}=81+\frac{360}{1\,000}=81,360$ .

Or, 360 millièmes est plus grand que 357 millièmes donc 81,36>81,357.

2. Rangement de deux nombres décimaux

Exemple :

Ranger les nombres 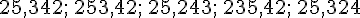$25,342;\,253,42;\,25,243;\,235,42;\,25,324$ dans l’ordre croissant.

On repère le plus petit, puis le plus petit des nombres qui restent, et ainsi de suite jusqu’au dernier.

On obtient donc .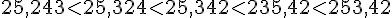

Définition :

Comparer deux nombres décimaux, c’est trouver lequel des deux est le plus grand ou dire si ils sont égaux.
Sur une demi-droite graduée, le plus grand nombre est celui qui est situé le plus à droite.

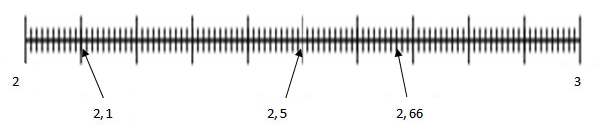
Exemple :

Nous souhaitons comparer 2,5 et 2,66.

On place ces deux nombres sur une demi-droite graduée.

On dit que 2,5<2,66 car 2,66 est situé le plus à droite sur la demi-droite graduée.

On dit que 2,5 est inférieur à 2,66 ou encore, que 2,66 est supérieur à 2,5.

Sinon sans droite graduée, il faut comparer les parties entières puis les parties décimales.

Ces deux nombres ont la même partie entière, nous devons comparer leur partie décimale.

Le chiffre des dixième est 5 pour 2,5 et 6 pour 2,66 donc 2,66>2,5.

Définition :

Comparer deux nombres, c’est trouver le plus grand, ou le plus petit, ou dire si ils sont égaux.

Définition :

Ranger des nombres dans l’ordre croissant , c’est les ranger du plus petit au plus grand.
Ranger des nombres dans l’ordre décroissant, c’est les ranger du plus grand au plus petit.

Exemple :

Ranger les nombres suivants 25 342, 253 420, 25 243, 235 420, 25 324 dans l’ordre croissant.

On repère le plus petit, puis le plus petit des nombres qu’il reste, et ainsi de suite jusqu’au dernier.

On obtient donc 25 243 < 25 324 < 25 342 < 235 420 < 253 420.

Définition :

Encadrer un nombre, c’est trouver un nombre plus petit et un nombre plus grand.
Ranger des nombres décimaux dans l’ordre croissant ( ou décroissant), c’est les ordonner du plus petit au plus grand ( ou du plus grand au plus petit).

Exemples :

Encadrement à l’unité de 7,13 : 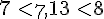$7\,<\7,13\,<8$

Encadrement au dixième de 7,13 :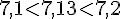

VII. Décomposition et nom des chiffres

Définition :

Tout nombre pouvant s’écrire sous la forme d’une fraction décimale, c’est à dire dont le numérateur est un nombre entier et le dénominateur est 1,10,100,1 000,10 000 …, est un nombre décimal.Il peut aussi se noter en utilisant une virgule, c’est son écriture décimale : elle est composée

d’une partie entière et d’une partie décimale.

Remarque :

Un nombre décimal a une partie décimale finie.

Exemple :

On considère le nombre décimal 1 345,824.

Ce nombre se lit mille-trois-cent-quarante-cinq unités et huit-cent-vingt-quatre-unités.
Il peut se décomposer sous la forme $1\,345,824=,(\,1\times \,1000\,\,)+\,\,(3\times \,100\,\,)+\,(\,4\times \,10\,\,)+\,(\,5\times \,1\,,)+\,(\,8\times \,\frac{1}{10}\,\,)+\,(\,2\times \,\frac{1}{100}\,\,)+,(\,4\times \,\frac{1}{1\,000}\,\,)$
Voici le nom de chaque chiffre :
1 est le chiffre des milliers
3 est le chiffre des centaines
4 est le chiffre des dizaines
5 est le chiffre des unités
8 est le chiffre des dixièmes
2 est le chiffre des centièmes
4 est le chiffre des millièmes.

Remarque :

Un nombre entier est un nombre décimal particulier.

En effet, 25 peut s’écrire avec une virgule 25=25,0 ou sous la forme d’une fraction décimale 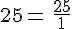$25=\,\frac{25}{1}$ .

0/5 - (30834 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «nombres décimaux : cours de maths en 6ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de 6ème

Volumes de solides

Le cercle

Fractions

Triangles et quadrilatères

Exercices de 6ème

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 13 928 271 cours et exercices de maths téléchargés en PDF et 4 250 exercices.