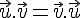Produit scalaire dans l’espace : cours de maths en terminale à imprimer en PDF.

Mis à jour le 20 décembre 2025

Sommaire

📚Cours de MathématiquesTerminale • lycée

Produit scalaire dans l’espace

⏱️Temps de lecture : 3 min

🎯Difficulté : Expert

📚Cycle terminal

📋Prérequis : Programme 1ère maîtrisé

📄Format PDF disponible gratuitement

Le produit scalaire dans l’espace à travers un cours de maths en terminale complet à télécharger en PDF. Vous devrez connaître les propriétés de linéarité et de symétrie du produit scalaire. Pouvoir déterminer si deux vecteurs sont colinéaires ou orthogonaux puis, déterminer l’équation d’une droite ou d’un plan connaissant un vecteur directeur ou un vecteur normal en terminale.

I. Le produit scalaire dans l’espace

1.Approche géométrique du produit scalaire

Définition :

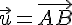
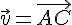
Soient $\vec{u}$ et $\vec{v}$ deux vecteurs de l’espace, et A,B,C trois points tels que $\vec{u}=\vec{AB}$ et $\vec{v}=\vec{AC}$ .Il existe au moins un plan P contenant les point A, B et C.

On appelle produit scalaire de $\vec{u}$ et $\vec{v}$ , le produit scalaire $\vec{AB}.\vec{AC}$ calculé dans le plan P.

Ainsi :

Si u et v sont non nuls,

$\vec{u}.\vec{v}=AB\times\,AC\times\,cos(\widehat{BAC})$ ;

Si u=0 ou v=0, le produit scalaire de u et v est nul : $\vec{u}.\vec{0}=0$ et $\vec{0}.\vec{v}=0$ .

Exemple :

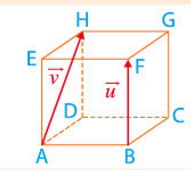
ABCDEFGH est un cube d’arête a.

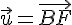
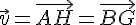
Soit $\vec{u}=\vec{BF}$ et $\vec{v}=\vec{AH}=\vec{BG}$ .

$\vec{u}.\vec{v}=\vec{BF}.\vec{AH}=\vec{BF}.\vec{BG}=BF\times\,BG\times\,cos(\widehat{FBG})$

donc $\vec{u}.\vec{v}=a\times\,a\sqrt{2}\times\,cos(\frac{\pi}{4})=a\times\,a\sqrt{2}\times\,\frac{\sqrt{2}}{2}=a^2$

Propriété:

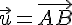
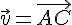
Si $\vec{u}$ et $\vec{v}$ sont deux vecteurs non nuls tels que $\vec{u}=\vec{AB}$ et $\vec{v}=\vec{AC}$ , alors :

$\vec{u}.\vec{v}=\vec{AB}.\,\vec{AC}=\vec{AB}.\,\vec{AH}=\vec{AK}.\,\vec{AC}$

où H est le projeté orthogonal de C sur la droite (AB) et K est le projeté orthogonal de B sur la droite (AC) .

Si $\vec{u}$ , $\vec{v}$ et $\vec{w}$ sont trois vecteurs de l’espace et k un nombre réel alors :

$\vec{u}.(\vec{v}+\vec{w})=\vec{u}.\vec{v}+\vec{u}.\vec{w}$
$\vec{u}.\vec{v}=\vec{v}.\vec{u}$
$(k\vec{u}).\vec{v}=\vec{u}.(k\vec{v})=k(\vec{u}.\vec{v)}$

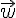
2.Caractérisation vectorielle de l’orthogonalité

Définition :

Deux vecteurs non nuls sont orthogonaux si, et seulement s’ils dirigent des droites orthogonales. Le vecteur nul est orthogonal à tous les vecteurs de l’espace.

Propriété :

Deux vecteurs

sont orthogonaux si, et seulement si,

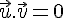
3.Expression analytique du produit scalaire

Propriété :

Dans un repère orthonormé (O, i, j, k) de l’espace, on considère les vecteurs $\vec{u}$ et $\vec{v}$ de coordonnées respectives (x, y, z) et (x’, y’, z’),Nous avons $\vec{u}.\vec{v}=xx'+yy'+zz'$ .

En particuliers, $\vec{u}.\vec{u}=x^2\,+y^2\,+z^2$ et $\left\,\|\vec{u}\,\right\,\|=\sqrt{\vec{u}.\vec{u}}=\sqrt{x^2\,+y^2\,+z^2}$ .

II. Applications du produit scalaire

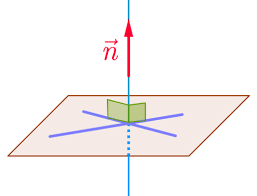
1.Vecteur normal à un plan

Définition :

Un vecteur $\vec{n}$ non nul est dit orthogonal à un plan si ce vecteur est un vecteur directeur d’une droite orthogonale à ce plan. Ce vecteur est alors appelé vecteur normal au plan.

Théorème :

Une droite (d) est orthogonale à toute droite d’un plan P si, et seulement si, elle est orthogonale à deux droites sécantes 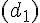(d_1) et (d_2) de ce plan.

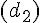
2.Equation cartésienne d’un plan

Propriété :

Soit un vecteur $\vec{n}$ non nul et A un point de l’espace. L’unique plan P passant par A et de vecteur normal $\vec{n}$ est l’ensemble des points M de l’espace tels que :

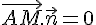
$\vec{AM}.\vec{n}=0$ .

Propriété :

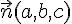
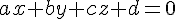
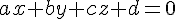
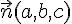
Dans un repère orthonormé, un plan P de vecteur normal $\vec{n}(a,b,c)$ a une équation de la forme .Réciproquement, si a, b et c ne sont pas tous les trois nuls, l’ensemble (E) des points M(x, y, z) tels que

est un plan de vecteur normal $\vec{n}(a,b,c)$ .

4.9/5 - (30726 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «produit scalaire dans l'espace : cours de maths en terminale à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de Terminale

Matrices et graphes

Fonctions cosinus et sinus

Suites numériques

Intégrale

Exercices de Terminale

logarithme neperien exercices maths terminale

Logarithme népérien

fonctions sinus cosinus exercices maths terminale

Fonctions sinus et cosinus

limites fonctions exercices maths terminale

Limites de fonctions

droites plans espace exercices maths terminale

Droites et plans de l’espace

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 631 747 cours et exercices de maths téléchargés en PDF et 4 250 exercices.