Proportionnalité : cours de maths en 5ème à imprimer en PDF.
Mis à jour le 25 janvier 2026
I. Quantités proportionnelles :
1. Définition et vocabulaire :
Deux grandeurs sont dites proportionnelles lorsque l’on peut passer de l’une à l’autre en multipliant par un même nombre non nul.
Si c’est le cas, ce nombre, noté 
Exemple :
La masse de viande (en kg) est-elle proportionnelle au prix du morceau de viande (en €)?
.
Tous les rapports sont égaux donc la masse (en kg) et le prix (en €) sont proportionnels et le coefficient de proportionnalité est 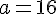
Exemple :
- La longueur du côté et le périmètre d’un carré sont proportionnels car le périmètre d’un carré s’obtient en multipliant la longueur de son côté par 4.
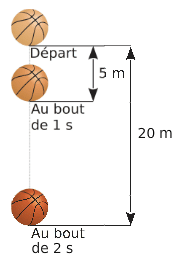
- Voici la distance parcourue par un ballon en chute libre. En 1 s, il parcourt 5 m et en 2 s, il parcourt 20 m. Pour passer de la durée de chute à la distance parcourue, on ne multiplie pas par un même nombre, donc la durée de chute et la distance parcourue par le ballon ne sont pas proportionnelles.
Remarque :
Ce tableau est appelé tableau de proportionnalité.
2.Tableau de proportionnalité
Exemple :
A la vitesse de 70 km/h, une voiture consomme 5 L aux 100 km.
- La consommation de carburant et la distance parcourue sont proportionnelles.
- A cette vitesse, quand la voiture parcourt une distance de 1 km, elle consomme 0,05 L. On peut regrouper ces résultats dans un tableau de proportionnalité.
- A cette vitesse, la consommation, en litres de carburant, est égale au produit du nombre de kilomètres parcourus par 0,05 qui est le coefficient de proportionnalité.
- Dans cette situation de proportionnalité, le coefficient permet de calculer la consommation à partir du nombre de kilomètres parcourus. Par exemple, à cette vitesse et pour 15 km, la consommation sera
L.
3. La quatrième proportionnelle :
Considérons le tableau de proportionnalité ci-dessous.
Le nombre 
Remarque :
Le nombre de places achetées et le prix (en €) sont proportionnels.
Pour calculer la valeur de la quatrième proportionnelle 
on utilise la règle du produit en croix :
€.
II. Les pourcentages :
1.Vocabulaire et définition :
Un pourcentage traduit une situation de proportionnalité.
Le quotient , que l’on note aussi t %, se lit t pour cent.
Exemple :
35%
50%
2.Calculer un pourcentage d’une quantité :
Exemple :
Calculer les 25 % de 216 €.
€.
Pour calculer 24% de 108 cm, on effectue :
cm.
3.Déterminer un pourcentage :
Exemple :
Dans un groupe de 25 employés, on compte 15 filles.
Calculer le pourcentage de filles.
On considère le tableau de proportionnalité suivante :
| Nombre employés | 25 | 15 |
| Pourcentage (en %) | 100 | 
|
Nous avons :
.
Conclusion : Il y a 60% de filles.
III. Applications de la proportionnalité
1.Appliquer à un pourcentage
Exemple :
Lors des soldes, une réduction de 15 % est accordée sur les articles d’un magasin.
Cela signifie que :
- la réduction et le prix initial d’un article sont proportionnels;
- si le prix initial d’un article est de 100 € alors la réduction est de 15 €.
On cherche la réduction d’un article coûtant 80 €. On regroupe ces données dans un tableau de proportionnalité.
Donc la réduction recherché est égale à 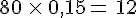
Exemple :
25 % de 350 est égal à .
2.Echelle
Exemple :
Ce dessin représente le plan d’un hélicoptère SA365 Dauphin.
Dans la réalité, il a pour hauteur 3,9 m, donc l’échelle est de :
.
Ce qui signifie que 1 cm sur plan correspond à 150 cm en réalité.
La longueur réelle de l’appareil est donc .
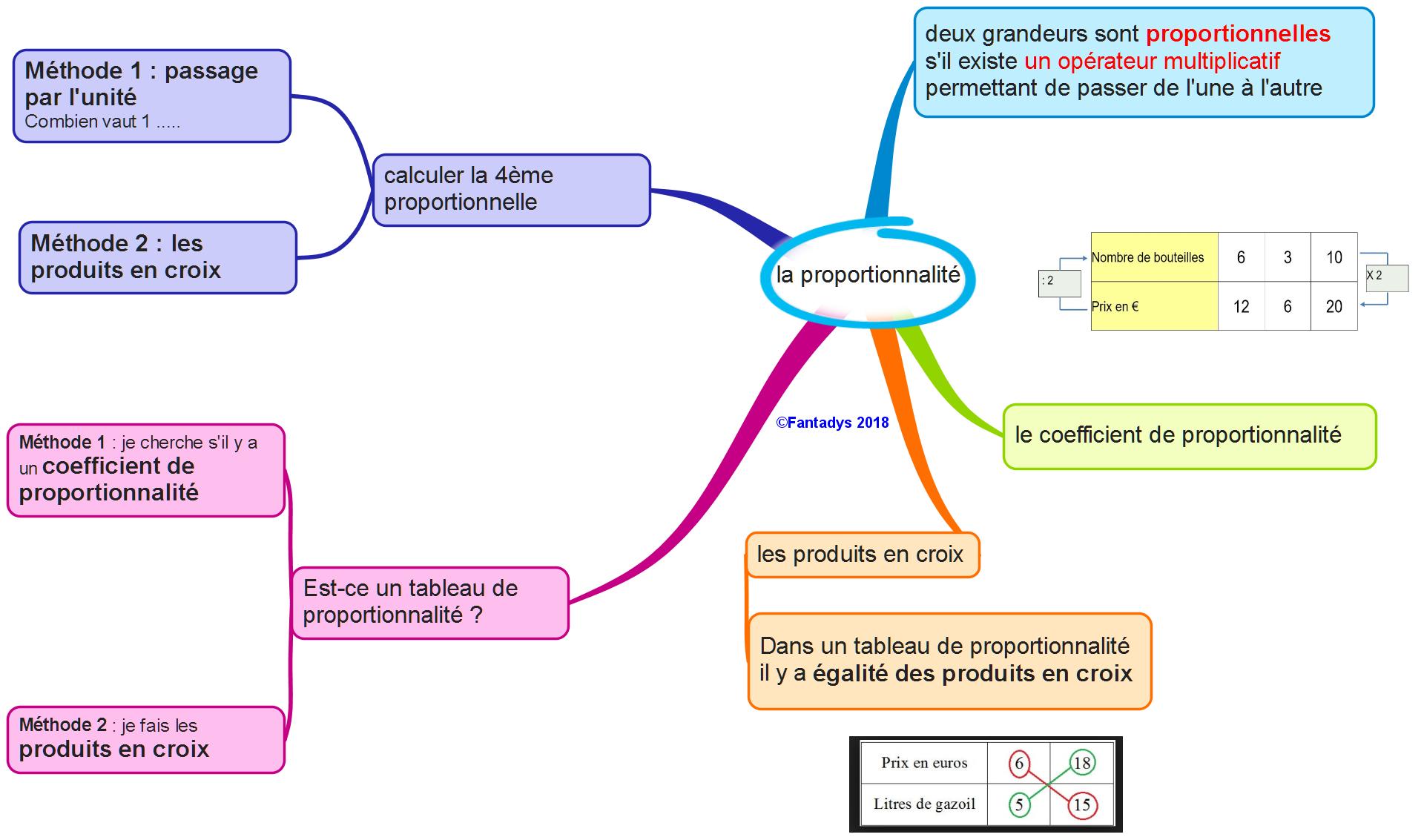
IV. Carte mentale sur la proportionnalité :
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «proportionnalité : cours de maths en 5ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Nos applications
Téléchargez la dernière version gratuite de nos applications.