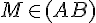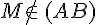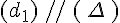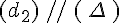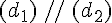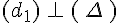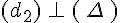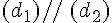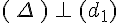Les droites parallèles et perpendiculaire : cours de maths en 6ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
Les droites parallèles et perpendiculaires à travers un cours de maths en 6ème en PDF. Nous aborderons le vocabulaire ainsi que les différentes notations et définitions ainsi que les méthodes de construction de droites parallèles ou perpendiculaires à la règle et au compas.
Nous terminerons cette leçon avec les trois propriétés fondamentales permettant de démontrer si deux droites sont parallèles ou perpendiculaires. Cette leçon reprend toutes les notions du programme officiel de l’éducation nationale en maths et permet aux élèves de sixième d’assimiler le contenu de leur leçon. L’élève sera amené à utiliser les symboles d’appartenance, de parallélisme et d’orthogonalité afin de justifier ou de démontrer si des droites sont parallèles ou perpendiculaires.
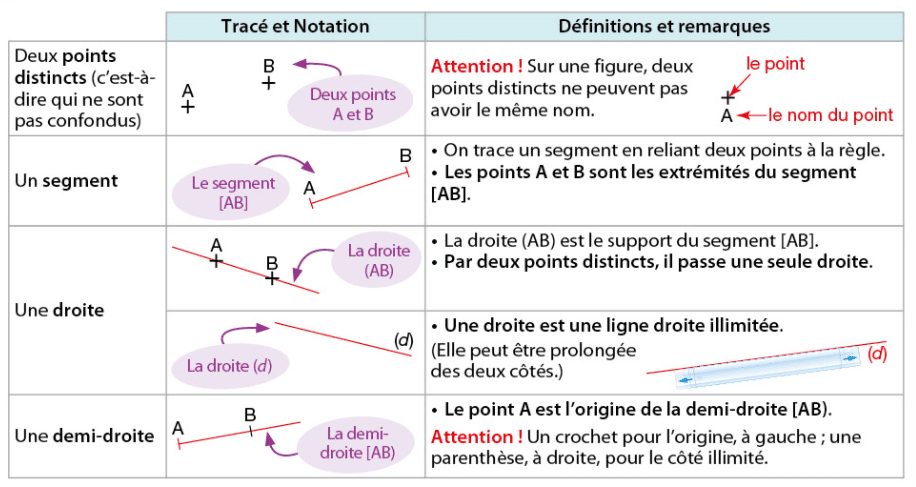
I. Point, segment, droite et demi-droite
1.Vocabulaire, représentations et notations
2. Alignement et appartenance
Exemple :
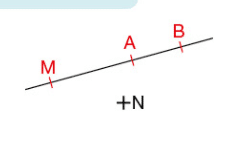
Sur la figure ci-dessous, les points A, B et M sont alignés.
- Le point M appartient à la droite (AB). On note
- Le point N n’appartient pas à la droite (AB).On note
3. Distance entre deux points
La distance entre deux points est la longueur du plus court chemin entre ces deux points. C’est la longueur du segment qui joint ces deux points.
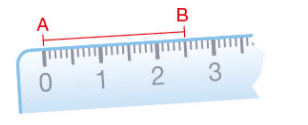
Exemple :
La distance entre les points A et B est de 2,5 cm.
On note : AB = 2,5 cm.
4. Milieu d’un segment
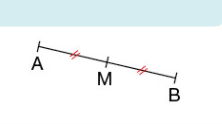
Exemple :
Le point M est le milieu du segment [AB].
En effet : les points A, M et B sont alignés et MA=MB.
II. Positions relatives de deux droites :
1. Droites sécantes :
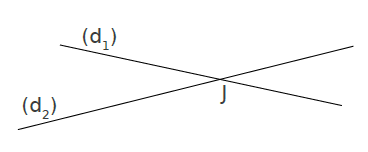
Exemple :
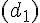
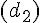
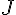
J est le point d’intersection de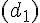
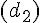
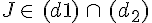
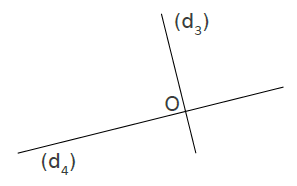
2. Droites perpendiculaires :
Deux droites perpendiculaires sont deux droites sécantes formant quatre angles droits .
Exemple :
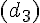
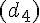
On note :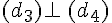 
Elles forment quatre angles droits .
3. Droites parallèles :
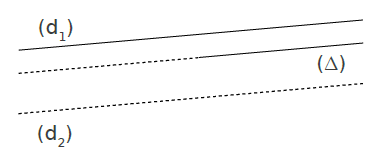
On dit que (d1) et (d2) sont strictement parallèles.2nd cas : (d3) et (d4) sont parallèles et tous leurs points sont communs.
On dit que (d3) et (d4) sont confondues.
On note : (d1) // (d2).On note : (d3) // (d4).
III. Constructions de droites
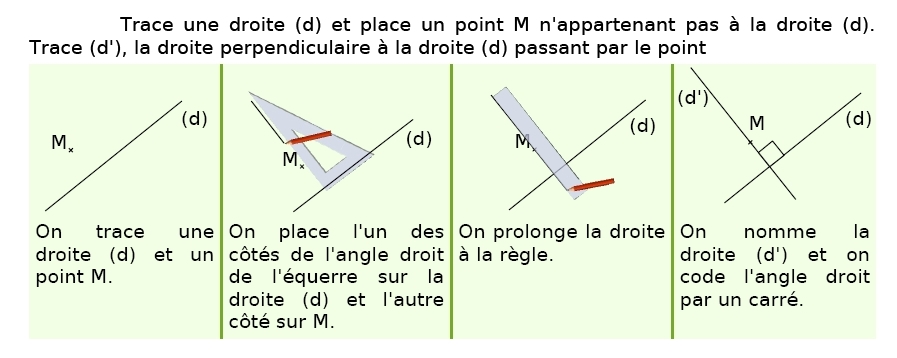
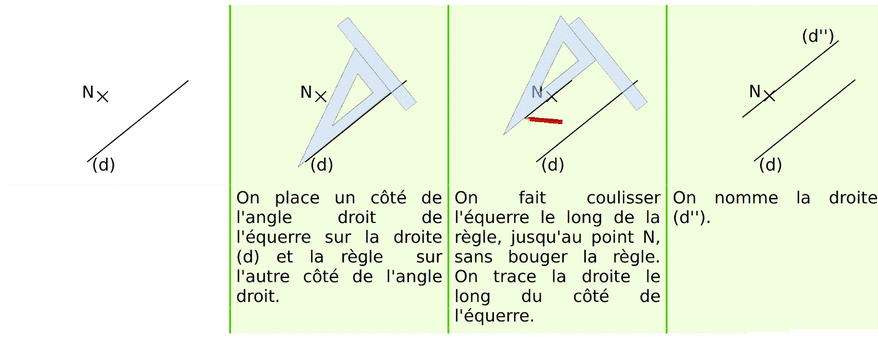
1. Droite perpendiculaire passant par un point
2. Droite parallèle passant par un point
IV. Les trois propriétés sur les droites parallèles et perpendiculaires :
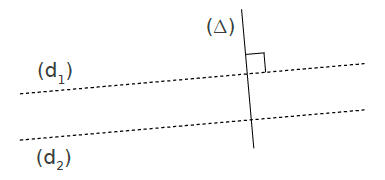
Si deux droites sont parallèles à une autre droite alors ces deux droites sont parallèles entre elles.
Je sais que : 
Donc je peux conclure que : 
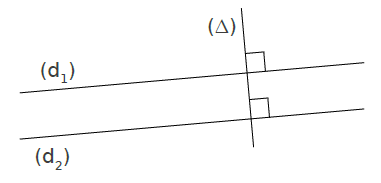
Si deux droites sont perpendiculaires à une autre droite alors ces deux droites sont parallèles entre elles.
Je sais que : 
alors cette troisième droite est perpendiculaire à l’autre.
Je sais que :
Télécharger ou imprimer cette fiche «les droites parallèles et perpendiculaire : cours de maths en 6ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 6ème
Exercices de 6ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.
