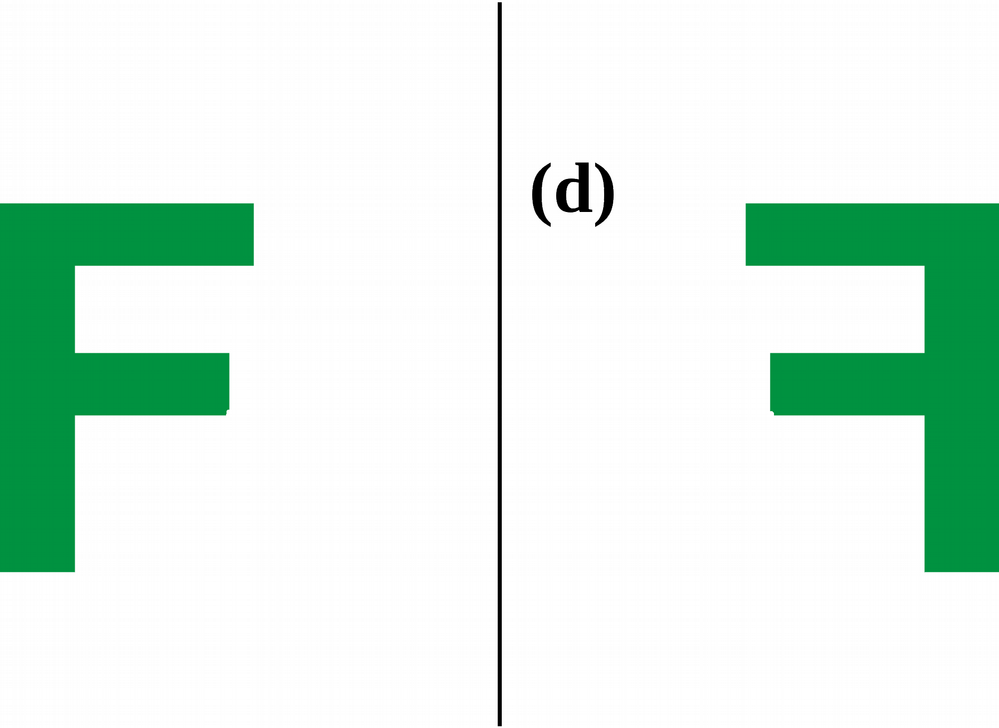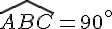Symétrie axiale : cours de maths en 6ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
I. Une première approche de la symétrie axiale :
1.Figures symétriques
Exemple :
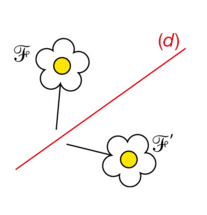
les figures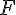 
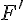
On dit aussi que :
2.Axe de symétrie d’une figure
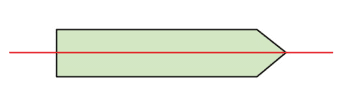
Exemple :
La droite rouge est l’axe de symétrie de cette figure.
La symétrie par rapport à une droite est aussi appelée symétrie axiale.
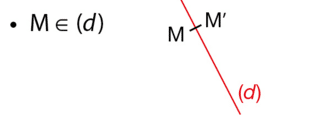
3.Symétrie d’un point
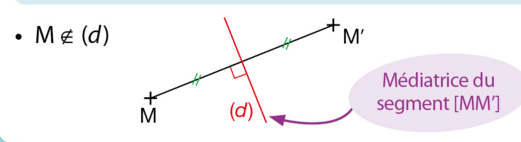
M n’appartient pas à (d).Le symétrique du point M par rapport à la droite (d) est le point M’ tel que la droite (d) soit la médiatrice du segment [MM’].
M appartient à (d).
Le symétrique du point M par rapport à la droite (d) est le point M lui-même.
II. Points symétriques par rapport à une droite :
1. Définition de points symétriques :
signifie que (d) est la médiatrice du segment [AB] .
Exemple :
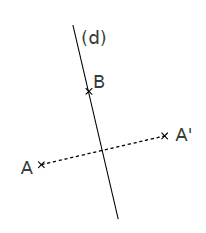
• A’ est le symétrique du point A par rapport à (d) ;
• A’ est l’image du point A par la symétrie d’axe (d) ;
• (d) est la médiatrice du segment [AA’].
Remarques :
• Le symétrique du point A’ est le point ….. .
• Tout point situé sur l’axe de symétrie a pour symétrique lui même.
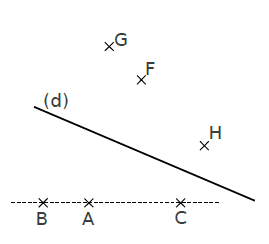
2. Construction à l’équerre et au compas :
- A l’équerre, on trace en pointillés la droite perpendiculaire à l’axe de symétrie passant par le point A.
- Au compas, on relève la distance entre le point A et l’axe de symétrie .
- Au compas, on reporte cette distance dans le secteur opposé du point A.
- On note le point symétrique A’.
III. Propriétés :
Une figure et sa figure symétrique sont superposables.
En conséquence, la symétrie axiale possède des propriétés de conservation.
1.Conservation des longueurs :
Le symétrique d’un segment est un segment ayant la même longueur.
Par conséquent, la symétrie axiale conserve les longueurs.
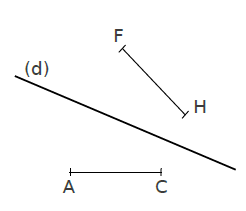
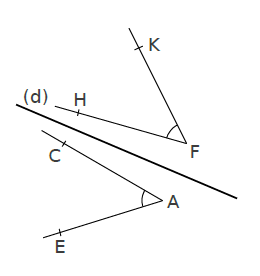
Exemple :
Le symétrique du segment [AC] est le segment [FH] et nous avons AC=FH .
2. Conservation de l’alignement :
3. Conservation de la mesure des angles :
4. Conservation de l’aire des figures :
La symétrie axiale par rapport à une droite conserve :
- les longueurs;
- l’alignement;
- les mesures d’angles;
- les aires.
Exemple :
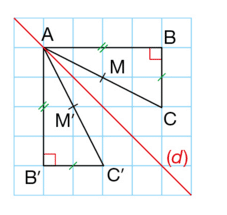
Les triangles rectangles ABC et AB’C’ ci-dessous sont symétriques par rapport à la droite (d).
- AB=A’B’, AC=A’C’, BC=B’C’.
- Le point M est aligné avec les points A et C.
Son symétrique M’ est aussi aligné avec les points A et C’.
- Les triangles ABC et A’B’C’ ont la même aire.
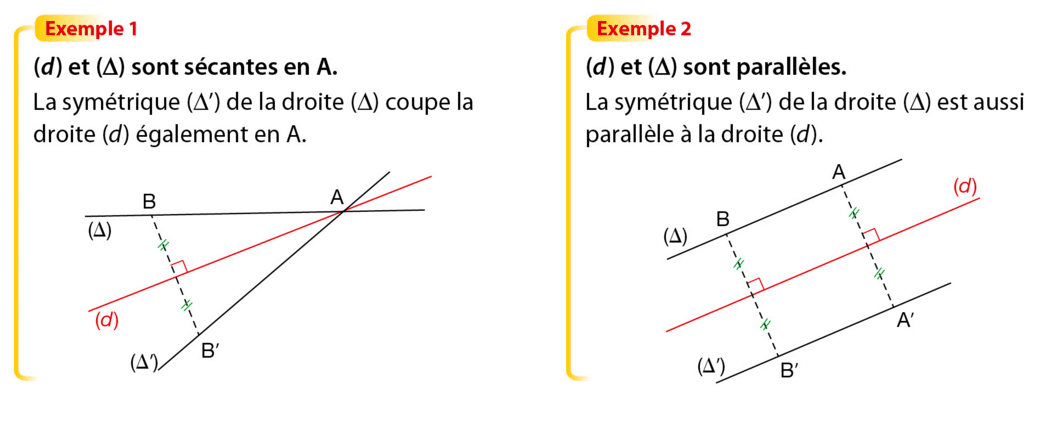
IV.Symétrique d’une droite et d’un segment
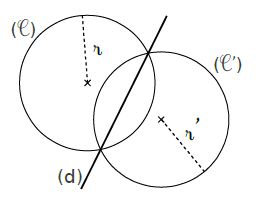
1.Symétrique d’une droite
2.Symétrique d’un segment
Le symétrique d’un polygone par rapport à une droite est un polygone qui a le même nombre de côtés.
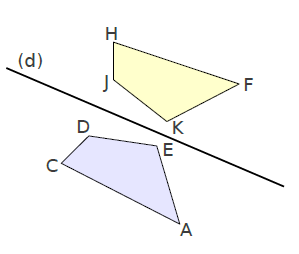
Exemple :
- Le symétrique par rapport à une droite d’un triangle est un triangle.
- Le symétrique par rapport à une droite d’un carré est un carré.
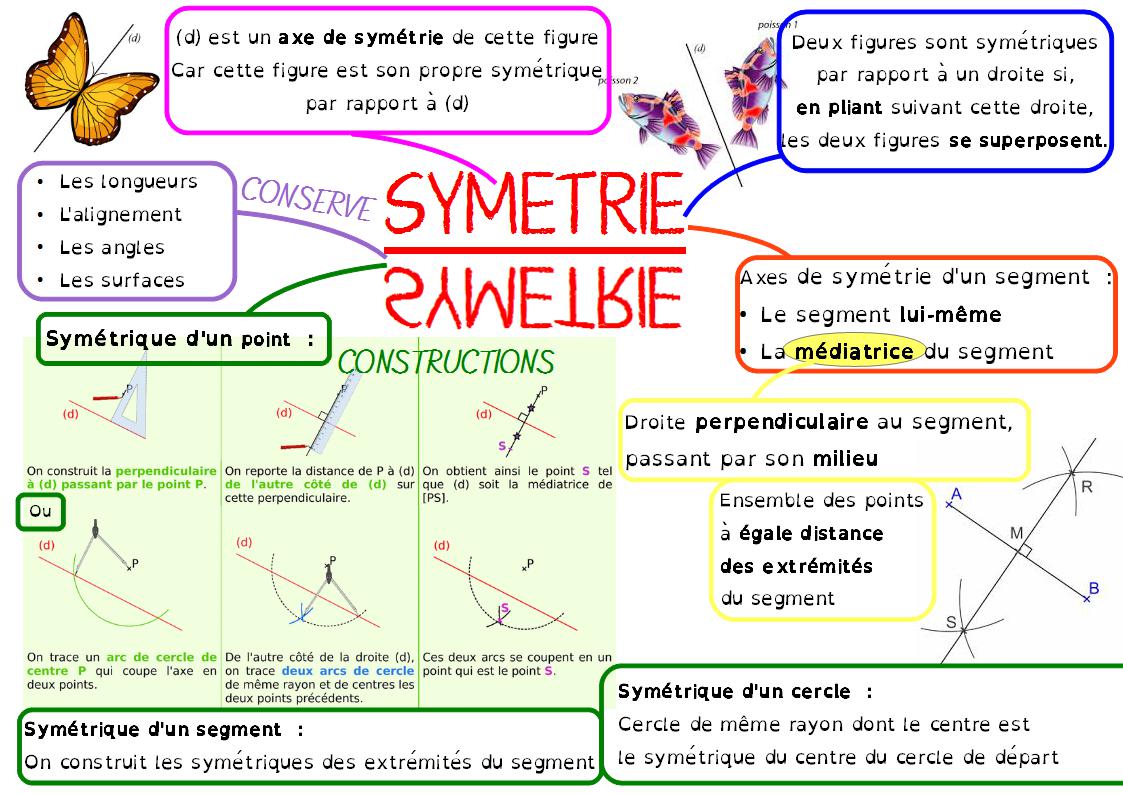
V. Carte mentale sur la symétrie axiale :
Télécharger ou imprimer cette fiche «symétrie axiale : cours de maths en 6ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 6ème
Exercices de 6ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.
