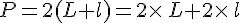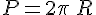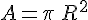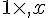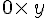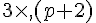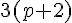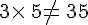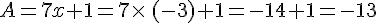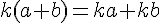Calcul littéral : cours de maths en 5ème à imprimer en PDF.

Mis à jour le 17 octobre 2025

Sommaire

📚Cours de Mathématiques5ème • collège

Calcul littéral

⏱️Temps de lecture : 5 min

🎯Difficulté : Intermédiaire

📚Cycle 4

📋Prérequis : Programme 6ème maîtrisé

📄Format PDF disponible gratuitement

Le calcul littéral avec un cours de maths en 5ème en PDF qui sera primordial pour la suite de votre scolarité. L’élève devra savoir simplifier des expressions algébriques mais également utiliser la propriété de simple distributivité afin de développer des expressions littérales en cinquième.

O. Introduction :

Le calcul littéral, calcul faisant intervenir des lettres, a été développé par le mathématicien Français François Viète (1540-1603).

Egalement appelé le calcul algébrique, c’est une généralisation du calcul numérique.

Vous avez souvent rencontré du calcul littéral lors de votre scolarité sans vous en rendre compte.

Notamment, en géométrie lors des calculs de périmètre et d’aire de figures géométriques.

Exemples :

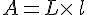
Aire d’un rectangle de longueur L et : $A=L\times \,l$ .

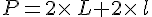
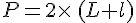
Périmètre d’un rectangle : $P=2\times \,L+2\times \,l$ ou $P=2\times \,(L+l)$ .

Périmètre d’un cercle de rayon R : 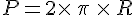$P=2\times \,\pi\,\times \,R$ .

I. Le calcul littéral : vocabulaire et définition.

1.Activité d’introduction :

2. Règles d’écriture et de simplification :

Règle :

En calcul littéral, afin de simplifier les écritures algébriques, nous ne noterons plus le signe $\times$ dans les situations suivantes :

lorsqu’il est situé entre deux lettres;
lorsqu’il est situé entre un nombre et une lettre;
lorsqu’il est suivi d’une parenthèse.

Exemples :

Simplifier les écritures littérales suivantes :

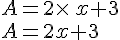
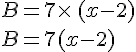
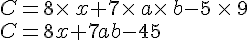
$A=2\times \,x+3\A=2x+3$ $B=7\times \,(x-2)\B=7(x-2)$ $C=8\times \,x+7\times \,a\times \,b-5\,\times \,9\C=8x+7ab-45$

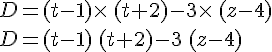
$D=(t-1)\times \,(t+2)-3\times \,(z-4)\D=(t-1)\,(t+2)-3\,(z-4)$

Définition :

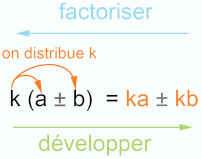
Développer une expression littérale, c’est l’écrire comme somme de termes.
Factoriser une expression littérale, c’est l’écrire comme produit de facteurs.

Exemples :

est une forme quelconque.

est une forme développée.

est une forme factorisée.

Définition :

Réduire une expression algébrique, c’est simplifier au maximum cette écriture en regroupant tous les termes de même nature.

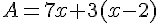
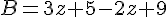
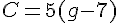
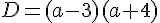
Exemples :

Réduire les expressions littérales suivantes :

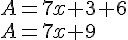
$A=7x+3+6\A=7x+9$

L’expression 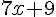7x+9 est appelée forme réduite.

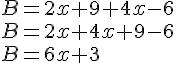
$B=2x+9+4x-6\B=2x+4x+9-6\B=6x+3$

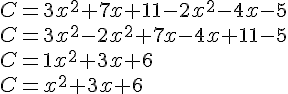
$C=3x^2+7x+11-2x^2-4x-5\C=3x^2-2x^2+7x-4x+11-5\C=1x^2+3x+6\C=x^2+3x+6$

II. La simple distributivité :

Propriété (simple distributivité) :

Pour tous nombres relatifs 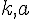k,a et , nous avons :

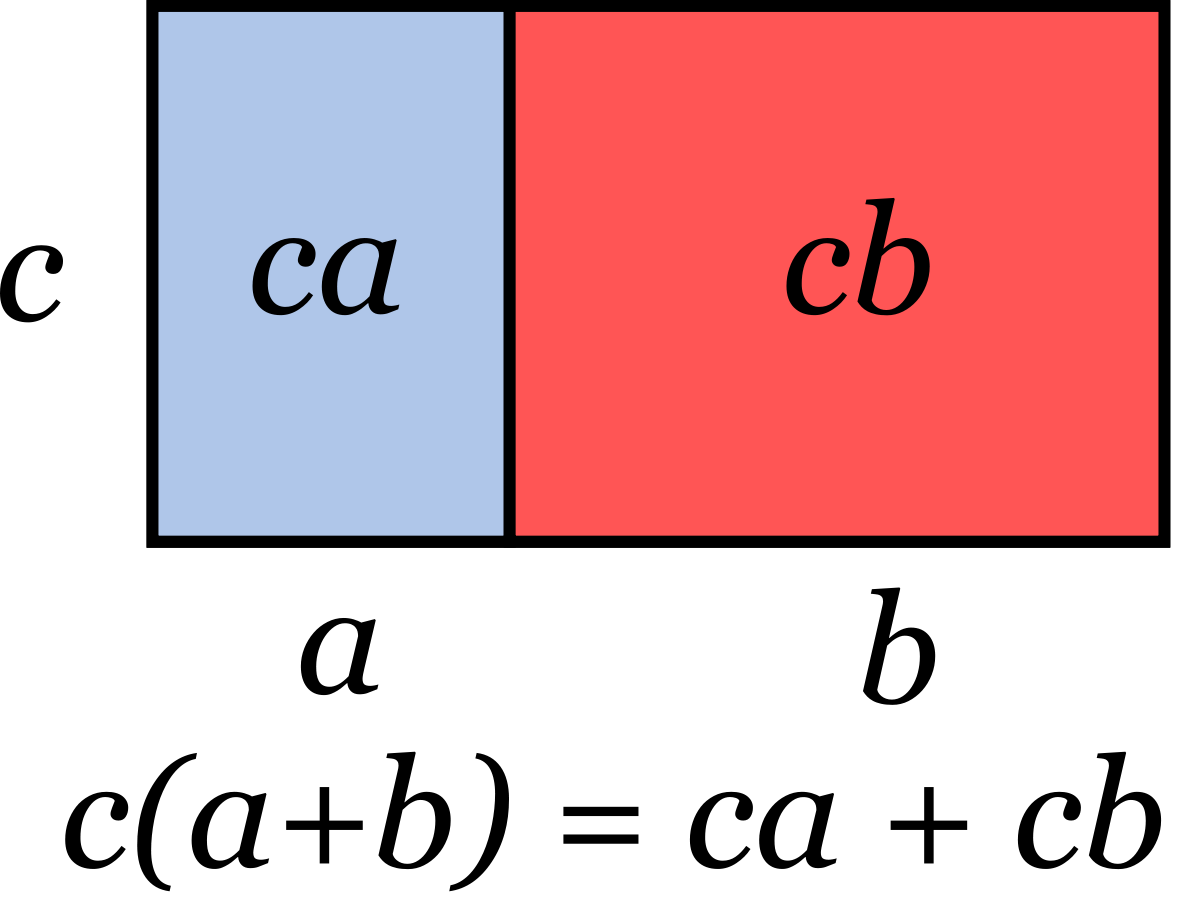
Preuve :

Exemples :

Développer et réduire des expressions :

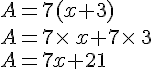
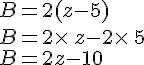
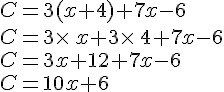
$A=7(x+3)\A=7\times \,x+7\times \,3\A=7x+21$ $B=2(z-5)\B=2\times \,z-2\times \,5\B=2z-10$ $C=3(x+4)+7x-6\C=3\times \,x+3\times \,4+7x-6\C=3x+12+7x-6\C=10x+6$

Calcul d’expression et substitution :

Calculer la valeur de A pour 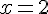x=2 puis, pour x=5 .

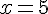
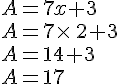
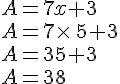
$A=7x+3\A=7\times \,2+3\A=14+3\A=17$ $A=7x+3\A=7\times \,5+3\A=35+3\A=38$

Test d’égalité :

L’égalité suivante est-elle vérifiée pour 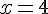x=4 ?

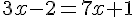
Calculons séparément :

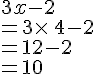
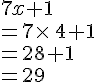
$3x-2\=3\times \,4-2\=12-2\=10$ $7x+1\=7\times \,4+1\=28+1\=29$

Nous en concluons que l’égalité n’est pas vérifiée lorsque 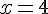x=4 .

III.Carte mentale sur le calcul littéral :

Autre version de cette leçon

I. Expression littérale du calcul littéral

Définition :

On appelle expression algébrique ou encore, expression littérale, toute expression mathématiques contenant des lettres. Ces lettres représentent des nombres.

Exemples :

L’aire d’un carré de côté c s’exprime avec l’expression littérale $A=c\times \,c=c^2$ .
Un rectangle de longueur L et de largeur l a un périmètre qui s’exprime avec l’expression littérale $P=2(L+l)=2\times \,L+2\times \,l$ .

Règle :

Nous ne noterons plus le signe $\times$ en calcul littéral :

entre deux lettres;
entre un nombre et une lettre;
avant l’ouverture d’une parenthèse;
après la fermeture d’une parenthèse.

Exemple :

Pour un rectangle de longueur L et de largeur l , son périmètre vaut $P=2(L+l)=2\times \,L+2\times \,l=2L+2l$ .
Un cercle de rayon R a pour périmètre $P=2\pi\,R$ et pour aire $A=\pi\,R^2$ .

Remarque :

On peut simplifier $1\times ,x$ en et $0\times \,y$ en .
L’expression $3\times ,(p+2)$ peut s’écrire .
Attention : on ne peut pas supprimer le signe x entre deux nombres $3\times \,5\neq\,35$ .

Définitions : puissances.

On considère un nombre positif a.

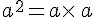
$a^2=a\times \,a$ , a^2 se lit « a au carré« .

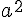
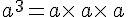
$a^3=a\times \,a\times \,a$ , a^3 se lit « a au cube« .

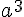
Exemple :

Aire d’un carré de côté a est 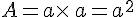$A=a\times \,a=a^2$ .

Le volume d’un cube de côté a est 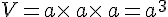$V=a\times \,a\times \,a=a^3$

II. Evaluer une expression littérale

Définition :

Pour calculer la valeur que prend une expression littérale, on substitue (remplace) la valeur de la lettre dans l’expression algébrique concernée.

Exemple :

Considérons l’expression littérale A=7x+1 .

Si x=3 alors $A=7x+1=7\times \,3+1=21+1=22$
Si x = -2 alors $A=7x+1=7\times \,(-3)+1=-14+1=-13$

On dit que l’on substitue (remplace) la valeur de x.

On passe, ainsi, du calcul littéral au calcul numérique.

III. Tester une égalité

Propriété :

Pour tester une égalité, il faut :

substituer la lettre par sa valeur dans le premier membre de l’égalité (expression située à gauche du signe =);
substituer la lettre par sa valeur dans le second membre de l’égalité (expression située à gauche du signe =);
si les résultats sont égaux alors l’égalité est vraie;
si les résultats ne sont pas égaux alors l’égalité est fausse.

Exemple :

Considérons l’égalité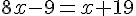

x = 7 vérifie-t-il cette égalité ?

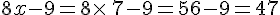
$8x-9=8\times \,7-9=56-9=47$ et .

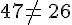
$47\neq\,26$ donc x = 7 ne vérifie pas cette égalité.

x = 7 vérifie-t-il cette égalité ?

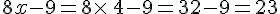
$8x-9=8\times \,4-9=32-9=23$ et .

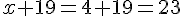
Donc x = 4 vérifie cette égalité.

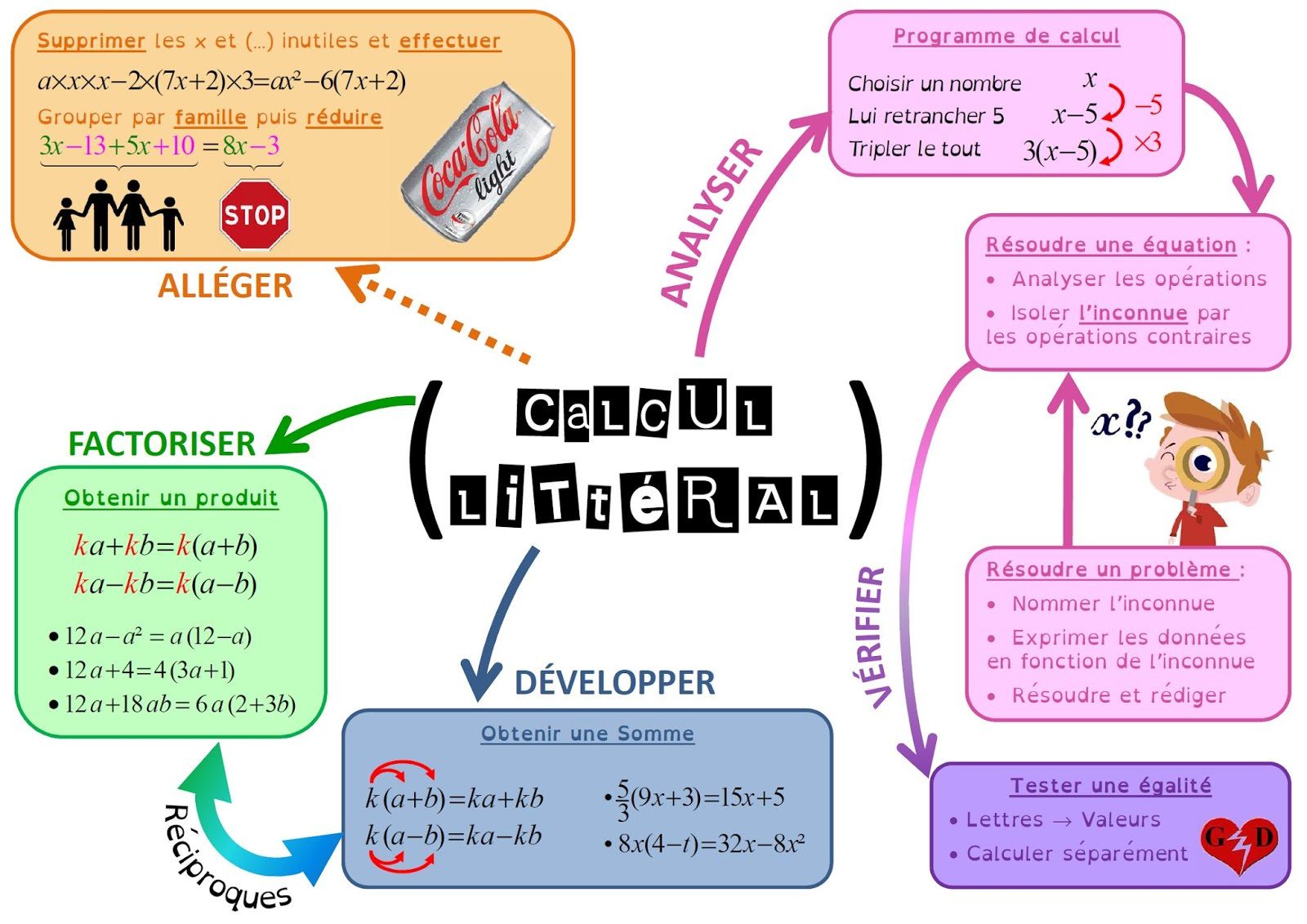
IV. La simple distributivité du calcul littéral

Définition :

Développer une expression littérale, c’est l’écrire comme somme de termes.

Exemple :

est une forme développée.

Définition :

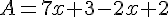
Factoriser une expression littérale, c’est l’écrire comme produit de facteurs.

Exemple :

sont des formes factorisées.

Définition :

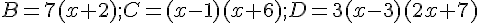
Réduire une expression littérale, c’est regrouper tous les termes de même nature.

Exemples :

Réduire les expressions suivantes :

Propriété :

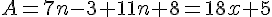
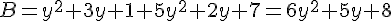
Soient k, a et b trois nombres relatifs :

Exemple :

En utilisant la simple distributivité, développer les expressions littérales suivantes :

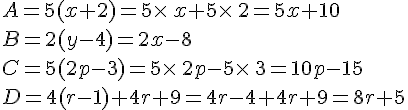
$A=5(x+2)=5\times \,x+5\times \,2=5x+10\B=2(y-4)=2x-8\C=5(2p-3)=5\times \,2p-5\times \,3=10p-15\D=4(r-1)+4r+9=4r-4+4r+9=8r+5$

4.9/5 - (31083 votes)

Télécharger puis imprimer cette fiche en PDF.

Télécharger ou imprimer cette fiche «calcul littéral : cours de maths en 5ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.

Cours de 5ème

Triangle

Symétrie centrale

Prisme droit et cylindre

Parallélogramme

Exercices de 5ème

Révise tous les chapitres de maths en ligne.

Exercices de maths interactifs avec saisie au clavier des réponses.

Espace game de maths et de programmation avec scratch, blockly et python du collège au lycée.

📚✏️

👥 8

🎓 L'équipe MATHS PDF

⚡ Mis à jour quotidiennement

👨‍🏫 8 Enseignants Titulaires 👩‍🏫

🏫 Collectif d'enseignants titulaires de l'Éducation Nationale en poste dans les écoles primaires, collèges et lycées.
📝 Notre équipe collaborative enrichit quotidiennement nos cours de maths et exercices corrigés.
✅ Expertise multi-niveaux • 📅 Contenu actualisé chaque jour • 🎯 Méthodes éprouvées

📚 Tous nos cours ✏️ Tous nos exercices

Nos applications

Téléchargez la dernière version gratuite de nos applications.

Maths PDF c'est 14 483 101 cours et exercices de maths téléchargés en PDF et 4 250 exercices.