Symétrie centrale : cours de maths en 5ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
I. Définitions et vocabulaire :
1.Activité d’introduction :
Deux figures 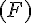
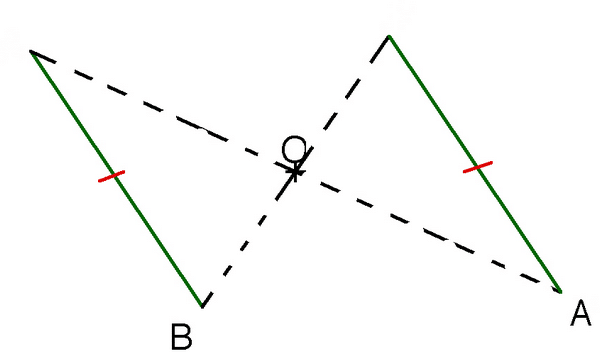
2.Symétrie centrale et demi-tour
Deux figures 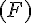
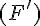
La figure 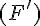
Exemple :
- La figure
- De même, la figure
- Les figures
- On dit également que le point O est le centre de la symétrie qui transforme la figure
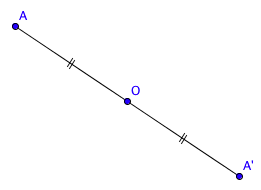
3. Le symétrique d’un point :
Exemple :
- Le symétrique de A par rapport à O est A’.
- Le symétrique de A’ par rapport à O est A.
- A et A’ sont symétriques par rapport à O.
Remarque :
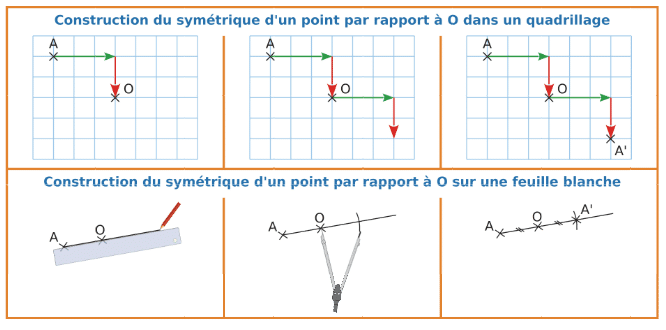
4.Méthode de construction du symétrique d’un point :
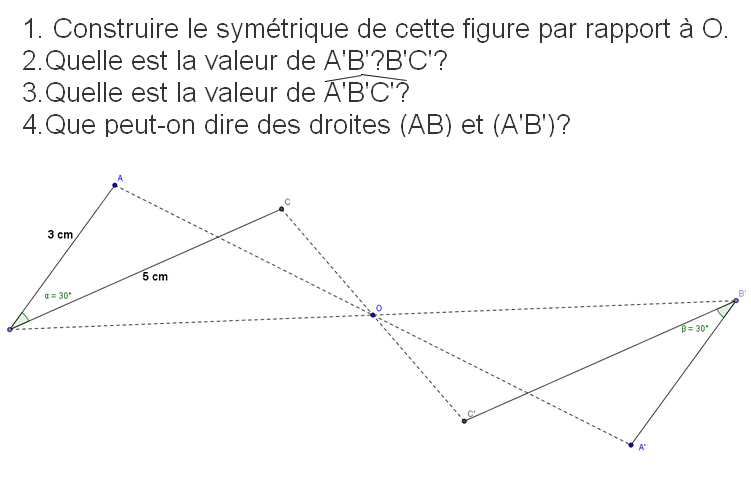
2. Symétrique d’un segment
- Le symétrique d’un segment par une symétrie centrale est un segment de même longueur.
- La symétrie centrale conserve les longueurs de segments, les périmètres et les aires de figures géométriques.
- Pour construire le symétrique du segment [CD] par rapport au point O, on construit le symétrique des points C et D, noté C’ et D’, par rapport au point O.
- Par la symétrie de centre O, le symétrique du segment [CD] est alors le segment [C’D’] .
- Le symétrique du milieu d’un segment est le milieu du segment symétrique.
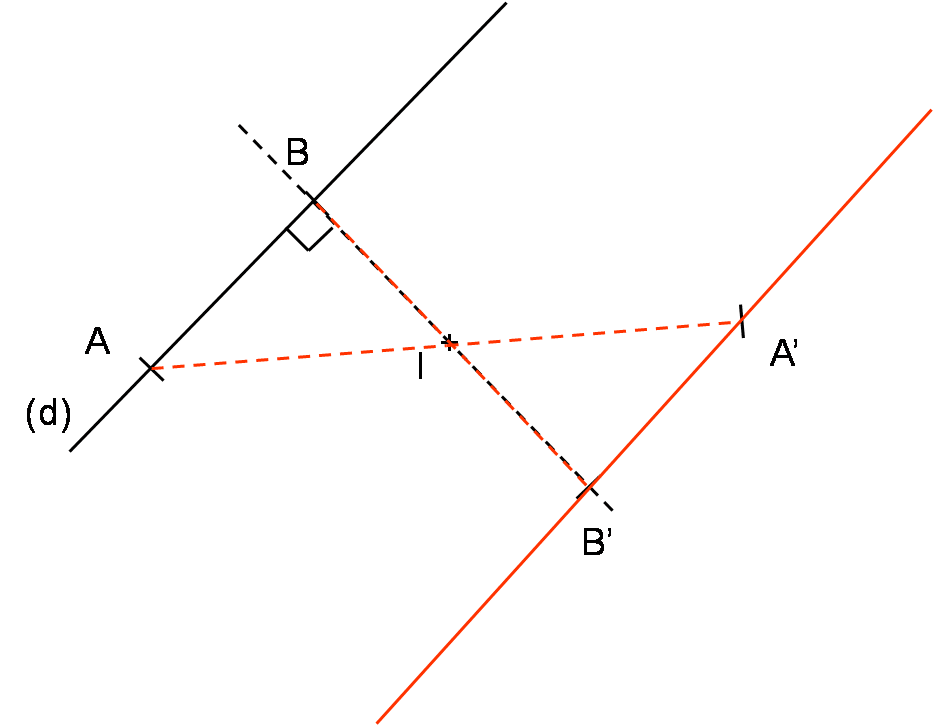
3. Symétrie d’une droite
- L’image d’une droite par une symétrie centrale est une droite qui lui est parallèle.
- La symétrie centrale transforme une droite en une autre droite qui lui est parallèle.
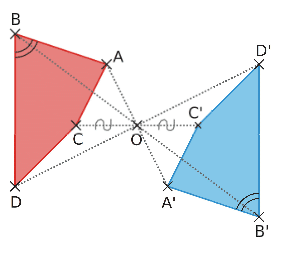
4. Symétrique d’un polygone
La symétrie centrale conserve tout, principalement :
- les longueurs;
- les périmètres de figures;
- les aires de figures;
- les mesures d’angles;
- le parallélisme;
- l’orthogonalité.
Le symétrique d’un polygone est un polygone possédant le même nombre de côtés et ayant la même forme.
Pour construire le symétrique d’un polygone, on construit le symétrique de chaque côté puis,
on relie les sommets dans le bon ordre.
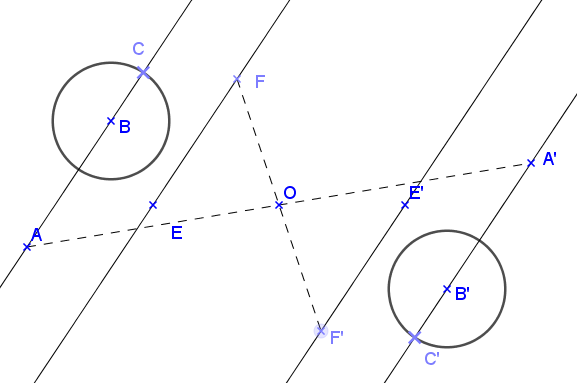
5. Symétrique d’un cercle
Remarque :
Pour construire le symétrique d’un arc de cercle par rapport à un point, on construit les symétriques du centre et des extrémités de l’arc de cercle symétrique.
6. Propriété de conservation :
La symétrie centrale conserve :
- les longueurs;
- les périmètres et aires;
- les mesures d’angles;
- l’alignement;
- le parallélisme;
- l’orthogonalité.
La symétrie centrale transforme :
- une droite en une autre droite qui lui est parallèle;
- un cercle en un autre cercle de même rayon.
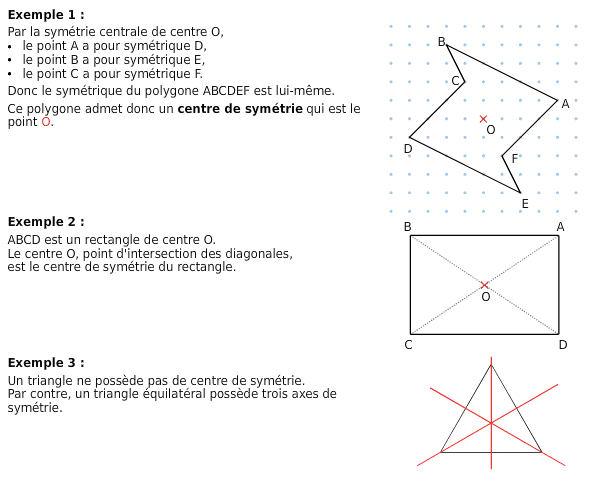
III.Centre de symétrie d’une figure
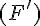
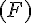
Télécharger ou imprimer cette fiche «symétrie centrale : cours de maths en 5ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Exercices de 5ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.