Fonctions convexe ou concave : cours de maths en terminale en PDF.
Mis à jour le 20 décembre 2025
I. Convexité d’une fonction
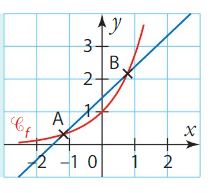
1. Sécante à la courbe représentative d’une fonction.

Soit A et B deux points de


2. Convexité et concavité.
Soit f une fonction et 
- f est convexe sur un intervalle I si, pour tout réel x de I,
- f est concave sur un intervalle I si, pour tout réel x de I,
3. Les fonctions usuelles.
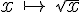
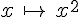
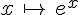
La fonction
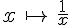

Exemple :
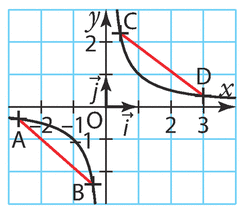
Soit f la fonction inverse définie sur 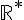
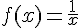

dans le repère ci-dessous.
Alors le segment [CD] est au-dessus de la courbe de 
convexe sur 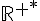

donc f est concave sur 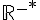
4.Position par rapport aux sécantes.
![t\in[0;1]](https://maths-pdf.fr/latex-images/960e35b2be2fb9fa717d8503ffedd24e.png)
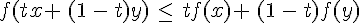
• Si f est une fonction concave sur un intervalle I alors pour tous réels x et y de I et pour tout t
![t\in[0;1]](https://maths-pdf.fr/latex-images/960e35b2be2fb9fa717d8503ffedd24e.png)
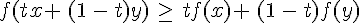
Démonstration :
Soient deux réels x et y et soit ![t\in[0;1]](https://maths-pdf.fr/latex-images/960e35b2be2fb9fa717d8503ffedd24e.png)
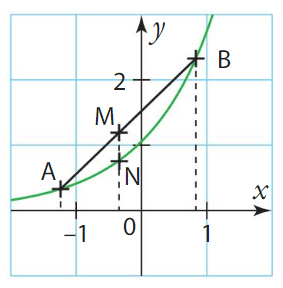
Soit 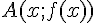
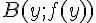
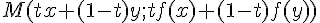

f étant convexe, cette sécante est située au-dessus de 
M est donc situé au-dessus du 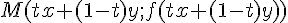
D’où 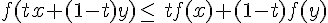
Remarque :
Si les inégalités précédentes sont strictes, on dira que f est une fonction strictement convexe ou strictement concave sur l.

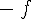
Exemple :
Soit fla fonction définie sur 
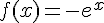
La fonction 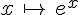
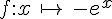
II. Fonction convexe et dérivées première et seconde
1.Fonction convexe et fonction concave.
Soit f une fonction deux fois dérivable sur I et
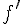
- f est convexe sur l, si et seulement si, pour tout réel x de l,
- f est concave sur l, si et seulement si, pour tout réel x de l,
Exemple :
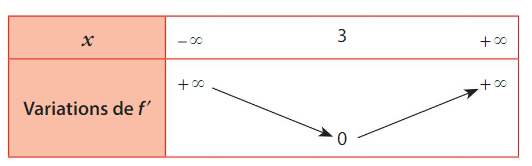
Soit f la fonction définie et dérivable sur 
On a dressé le tableau de variations de la fonction 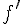
Alors f est concave sur ![]-\infty\,;\,3]](https://maths-pdf.fr/latex-images/6d6c3a579b0901955822d76977a30f0f.png)
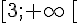
2.La fonction dérivée seconde.
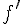
On appelle dérivée seconde de la fonction f, notée
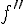
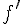
Exemple :
Soit f la fonction définie (et dérivable deux fois) sur 
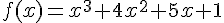
Alors 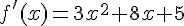
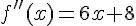
Remarques :
- La dérivée seconde d’une fonction affine est toujours nulle.
- La fonction exponentielle est égale à sa dérivée, donc à sa dérivée seconde également.
3.Convexité et dérivée seconde.
Soit f une fonction supposée deux fois dérivable et 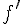
- f est convexe sur I si et seulement si, pour tout réel x de l,
- f est concave sur I si et seulement si, pour tout réel x de l,
Démonstration :
f’ est croissante (resp. décroissante) si et seulement si est 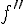
Donc f est convexe (resp. concave) si et seulement si 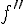
III. Tangente et point d’inflexion
1.Dérivée seconde et tangente.
Soit f une fonction supposée deux fois dérivable sur I de dérivée seconde 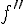
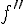
Preuve :
Soit 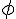
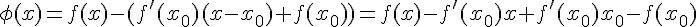
Alors 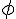
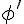
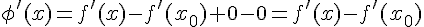
Or 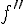
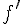
si 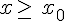
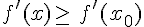
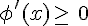
si 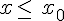
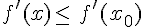
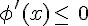
De plus, 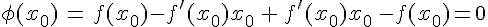
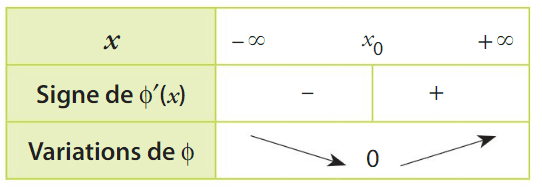
On obtient le tableau de variations ci-dessous.
Donc, pour tout réel x de I, 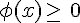
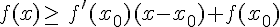
Conclusion :
Si 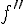
Remarques :
- Si
- Attention à la réciproque, une fonction convexe n’est pas obligatoirement deux fois dérivable.
2.Point d’inflexion à la courbe représentative d’une fonction.

dans un repère orthonormé du plan.
Soit A un point de

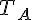

On dit que A est un point d’inflexion pour


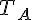
Exemple :
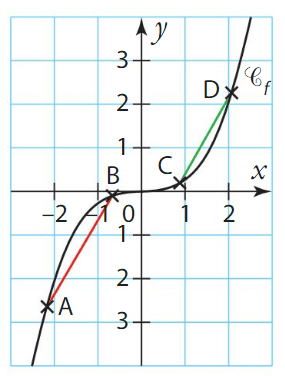
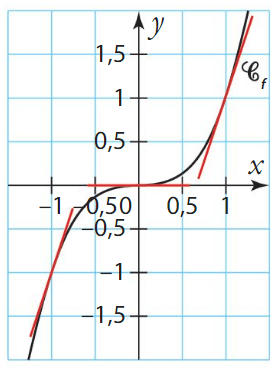
Soit f la fonction cube et 
Alors l’origine du repère 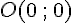

En revanche les tangentes en -1 et en 1 ne traversent pas la courbe, les points de coordonnées 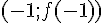
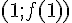
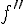
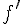
Exemple :
Si 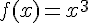
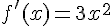
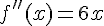
Donc 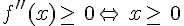
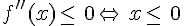
Il y a changement de signe de la dérivée seconde, donc f change de convexité, il y a donc en 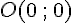
Télécharger puis imprimer cette fiche en PDF.
Télécharger ou imprimer cette fiche «fonctions convexe ou concave : cours de maths en terminale en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de Terminale
Exercices de Terminale
Nos applications
Téléchargez la dernière version gratuite de nos applications.