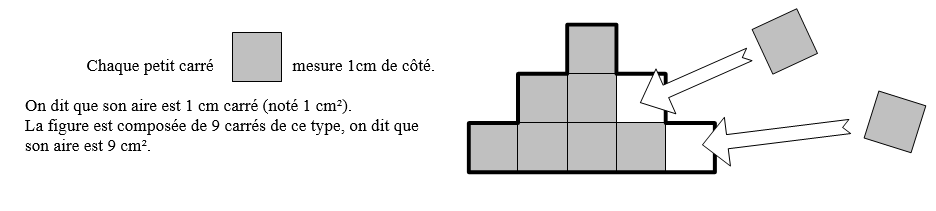
Périmètres et aires de figures : cours de maths en 6ème à imprimer en PDF.
Mis à jour le 20 décembre 2025
Le périmètres d’un objet bidimensionnel est la longueur totale de la frontière qui entoure l’objet. En d’autres termes, il s’agit de la distance autour de l’extérieur de l’objet.
I. Comparer et mesurer des périmètres :
Le périmètre d’une figure est la longueur de son contour.Il s’exprime à l’aide d’une unité de longueur.
Exemple :
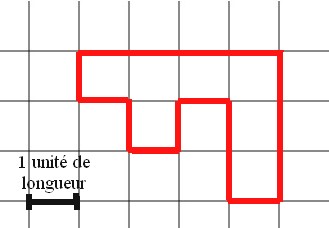
Le périmètre de la figure ci-dessous, exprimé en unité de longueur, est :
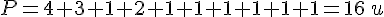
Le périmètre est de 16 unités de longueur.
Exemple :
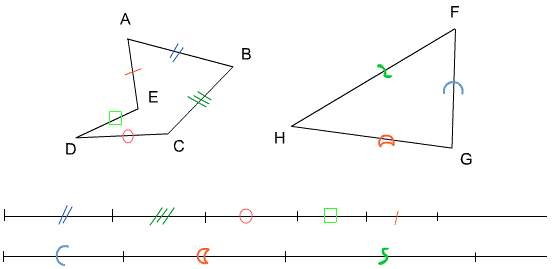
Parmi ces deux polygones, quel est celui qui possède le plus grand périmètre?
En observant les reports effectués au compas, nous en concluons que le triangle est celui qui possède le plus grand périmètre.
Exemple :
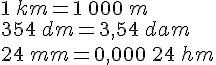
II.Périmètre d’un polygone :
1.Point de vue général :
Exemple :
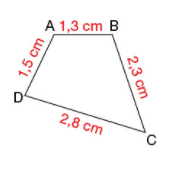
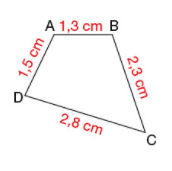
Calculer le périmètre du polygone en centimètres.
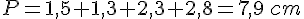
Exemple : périmètre d’un polygone.
Pour calculer le périmètre P de ce polygone, on additionne les longueurs de chaque côté.

Le périmètre de ce polygone est de 7,9 cm.
2.Périmètre d’un carré :
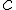

3.Périmètre d’un rectangle :
Soit un rectangle de largeur l et de longueur 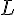

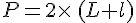
Exemple :
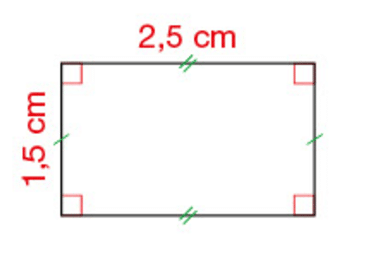
Le périmètre P du rectangle représenté ci-dessous est :
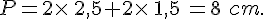
Le périmètre de rectangle est de 8 cm.
Exemples :
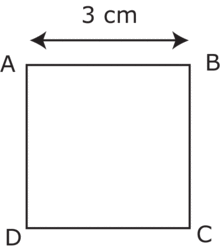
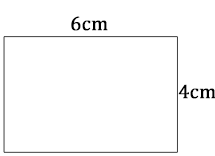
Calculer le périmètre du carré puis, celui du rectangle.
Les résultats seront exprimés en centimètres.


Remarque :
la multiplication est prioritaire devant l’addition.
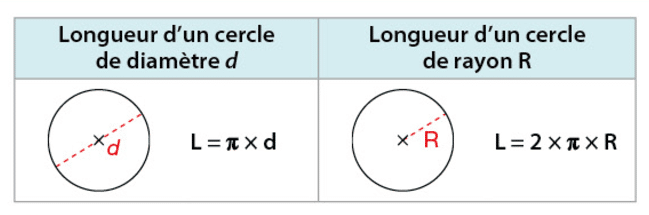
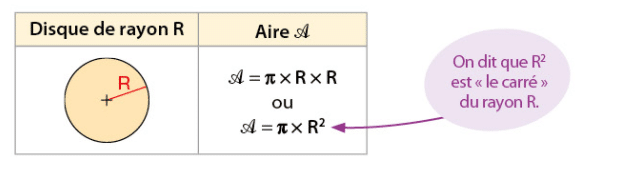
4.Périmètre d’un cercle :
Soit 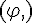
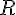
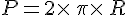
avec 
Remarque :
La lettre 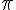
Exemple :
Calculer le périmètre du cercle suivant, le résultat sera arrondi à l’unité.
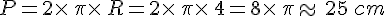
Exemple :
Le périmètre d’un cercle de rayon 3 cm est 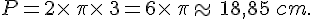
III. Aires de figures géométriques :
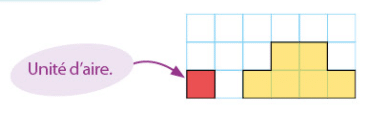
1.Unités d’aires de figures géométriques :
L’aire d’une figure géométrique est la mesure de la surface intérieure, dans une unité donnée.
Deux figures ayant la même aire n’ont pas forcément le même périmètre.
La réciproque est fausse aussi.
Exemple :
Remarque :
- Une aire s’exprime en « unités de longueur – carré » (m², cm², km²…)
- L’aire d’une figure géométrique est aussi appelée surface ou superficie.
- L’unité principale de mesure d’une aire est le mètre carré
Pour mesurer un terrain, on utilise :
L’are : 1 are = 1a = 1 dam2 = 100 m2
L’hectare : 1 hectare = 1ha = 1 hm2 = 100 dam2 = 10 000m2 = 100 ares
Exemple :
L’aire de la figure ci-dessous est égale à six unités.
Autres unités d’aire
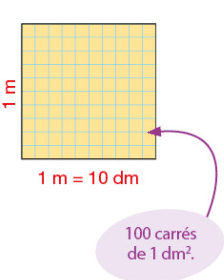
Le décimètre carré (dm²) est l’aire d’un carré de côté 1 dm.
Un carré d’aire 1 m² contient 100 carrés d’aire 1 dm².
Donc 
Pour mesurer la superficie des terrains, on utilise l’are (a) et l’hectare (ha) :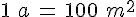
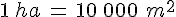
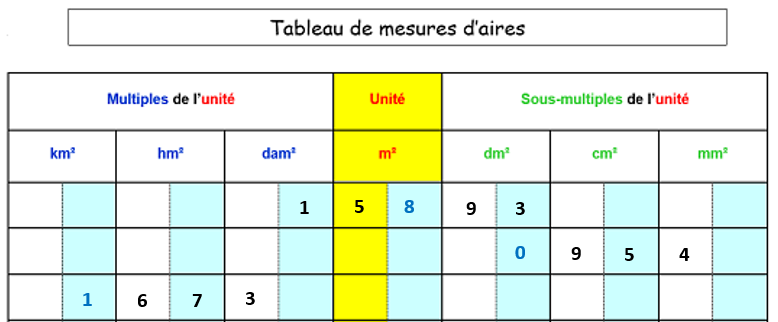
2.Tableau de conversion des aires :
Exemple :
Convertir les aires.
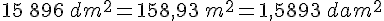
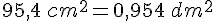
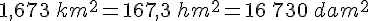
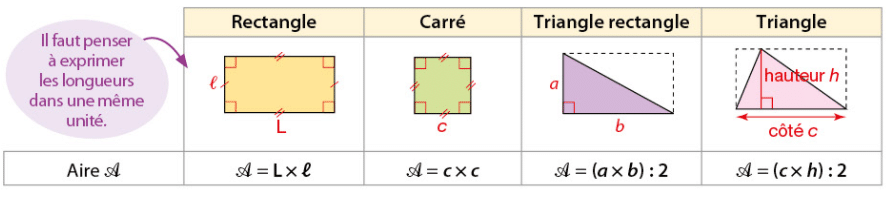
3.Aire d’un carré :
Propriété :
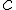

Remarque :
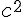
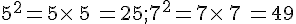
4.Aire d’un rectangle :
Soit un rectangle de largeur l et de longueur 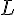
Son aire est 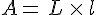
Exemples :
Calculer l’aire du carré puis, celui du rectangle.
Les résultats seront exprimés en cm².
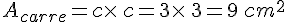

IV.Les durées
1.Durée
La mesure du temps entre deux instants s’appelle la durée. Une unité de durée souvent utilisée est la seconde (s).
Autres unités de durée :
Exemple :
Une séance de cinéma commence à 17 h 40 et se termine à 19 h 10.
Sa durée est 20 min + 1 h 10 min=1 h 30 min.
Cette séance a donc duré 1 h 30 min.
Télécharger ou imprimer cette fiche «périmètres et aires de figures : cours de maths en 6ème à imprimer en PDF.» au format PDF afin de pouvoir travailler en totale autonomie.
Cours de 6ème
Nos applications
Téléchargez la dernière version gratuite de nos applications.