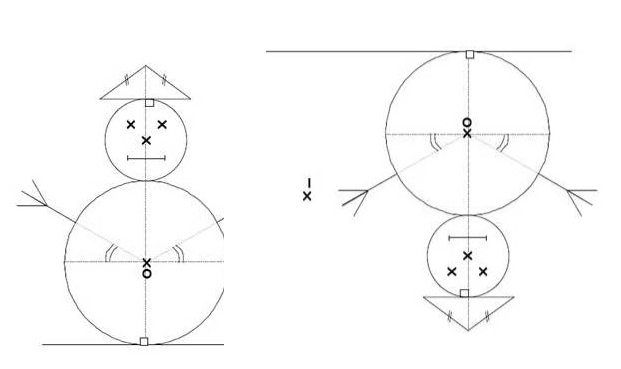
Exercice 1 : symétrie centrale – bonhomme de neige.
Construire la symétrique de la figure par rapport au point :
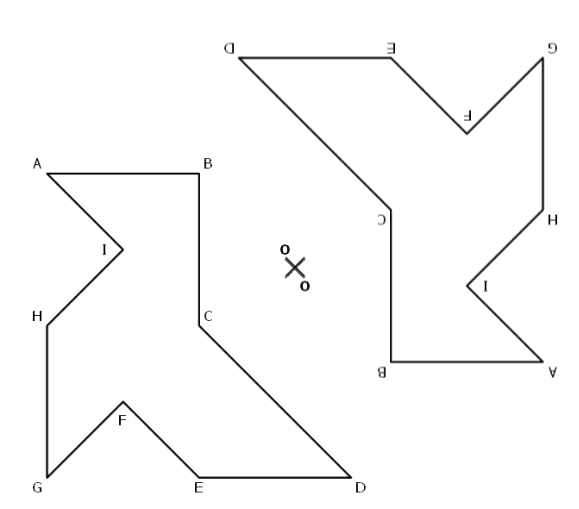
Exercice 2 : symétrie centrale – chaussures.
Construire l’image de la figure par rapport au centre consiste à effectuer une symétrie centrale par rapport au point
.
Chaque point de la figure d’origine sera déplacé pour que le point soit le milieu du segment qui relie le point d’origine et son image.
On obtient ainsi l’image symétrisée de la figure d’origine.
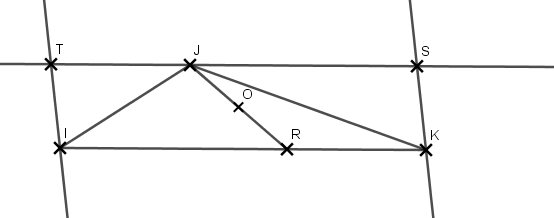
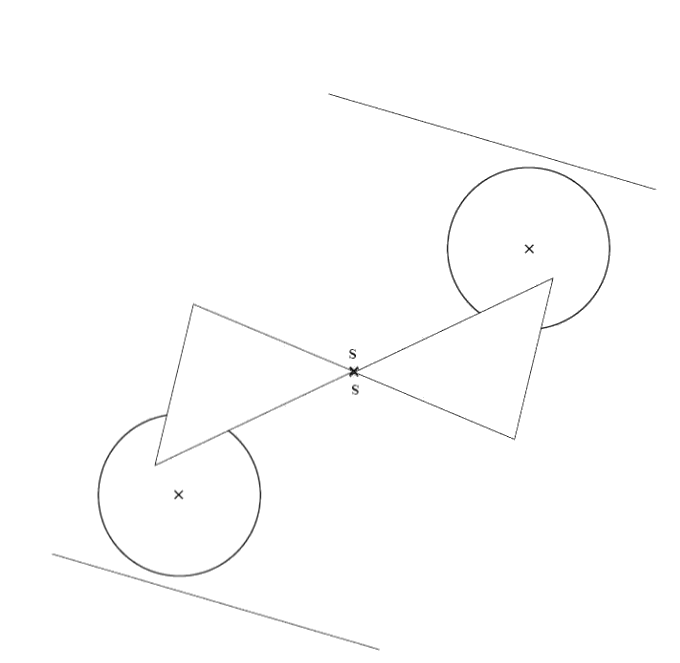
Exercice 3 : symétrie centrale et propriétés
1.
2. Les droites et
sont parallèles et les longueurs
et
sont égales.
Démonstration 1 :
On sait que :
Les droites (TI) et (KS) sont symétriques par rapport à O.
Propriété :
La symétrie centrale transforme une droite en une autre droite qui lui est parallèle.
Conclusion :
Les droites et
sont parallèles.
Démonstration 2 :
On sait que :
Les segments [TI] et [KS] sont symétriques par rapport à O.
Propriété :
La symétrie centrale conserve la longueur des segments.
Conclusion :
Les longueurs et
sont égales.
3. Les mesures des angles et
sont égales.
Démonstration :
Comme est le milieu de
et que
est sur
, par symétrie, les angles formés par les segments sont conservés :
4. Les points ,
et
sont alignés.
Démonstration :
Le point étant le milieu de
, le point
étant sur
, et par symétrie des points
et
par rapport à
, les points peuvent être considérés alignés via le chemin
–
–
.
Propriété :
La symétrie centrale conserve l’alignement.
Comme est sur la droite
par construction, on obtient que
,
, et
sont alignés.
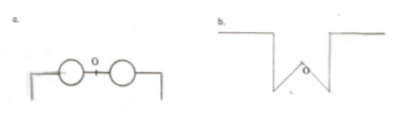
Exercice 4 : propriétés de la symétrie centrale – démontrer
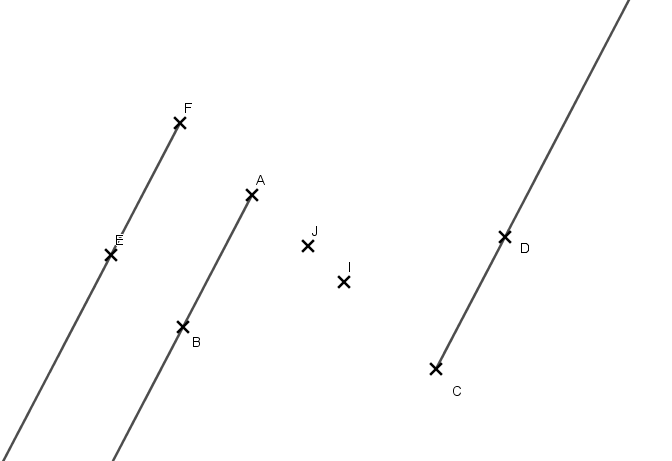
2. La symétrique de la demi-droite par rapport au point
est la demi-droite
.
3. La symétrique de la demi-droite par rapport au point
est la demi-droite
.
– En utilisant les propriétés des symétries centrales, puisque est le symétrique de
par rapport à
, et
celui de
, les segments
et
sont parallèles.
– Les demi-droites et
sont même opposé.
Exercice 5 : centre de symétrie d’une figure
Exercice 6 : symétrie centrale d’une figure.
Exercice 7 : symétrie centrale d’une figure
Pour répondre à l’exercice demandé, voici la correction :
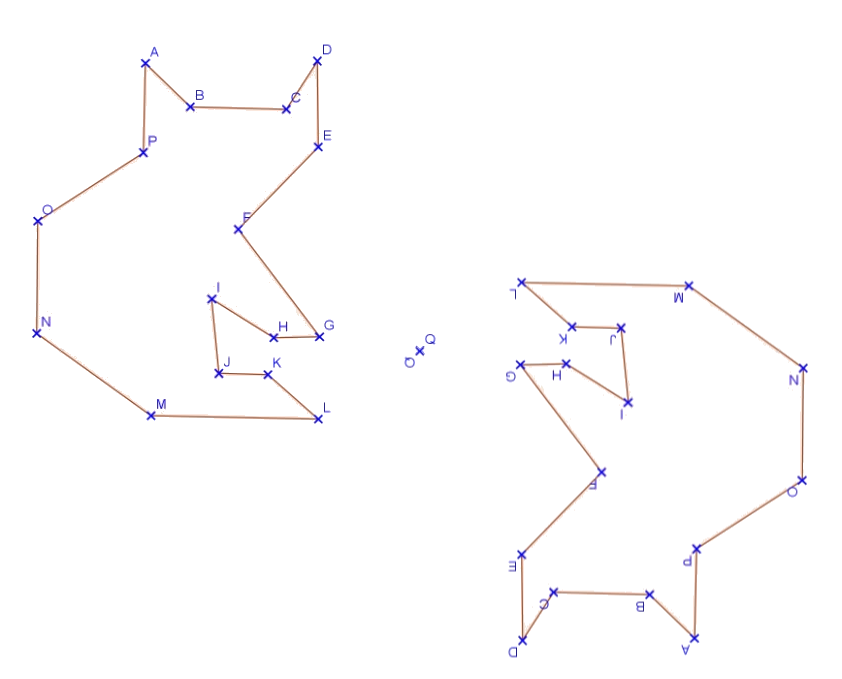
Exercice 8 : symétrie centrale d’un chat
Pour construire la figure symétrique du chat par rapport au point , il faut construire les symétriques pour chaque point du chat:
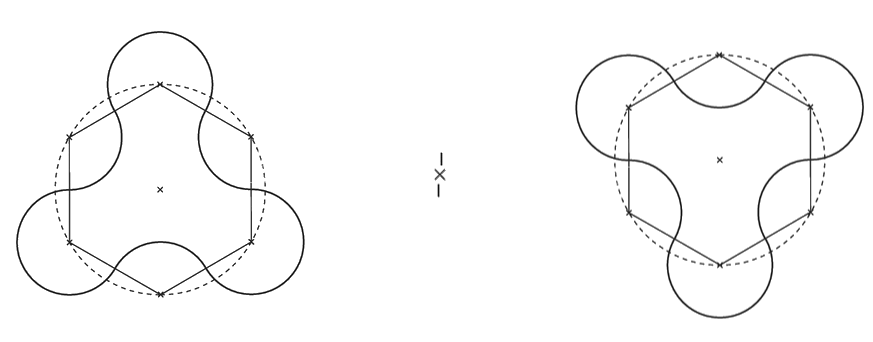
Exercice 9 : symétrie centrale de cercles
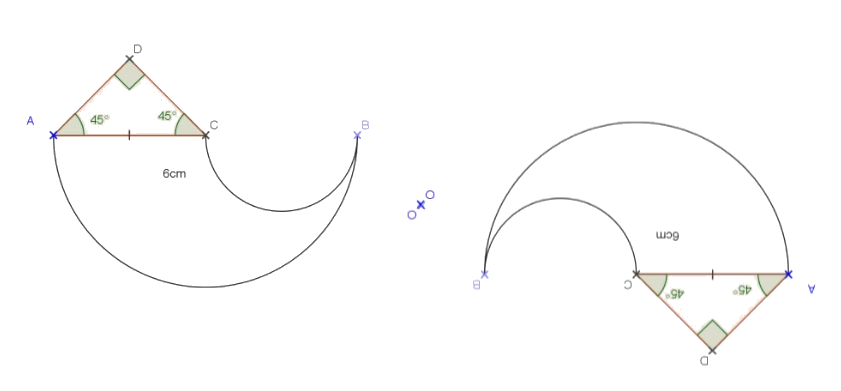
Exercice 10 : construction de symétries centrales
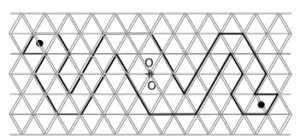
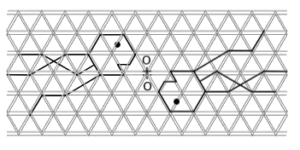
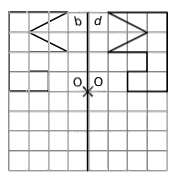
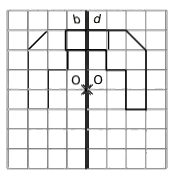
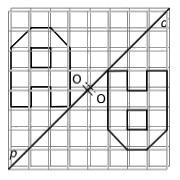
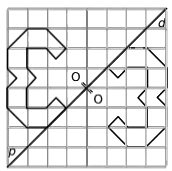
Remarques : Assurez-vous de prendre en compte la distance proportionnelle entre chaque point et l’axe de symétrie pour garantir une réflexion correcte.
Exercice 11 : propriétés de la symétrie centrale
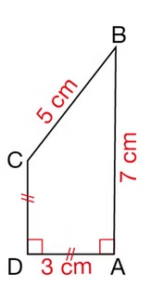
1. Donner, en justifiant, chaque longueur :
Propriété :
La symétrie centrale conserve la longueur des segments.
a.
Comme et
sont les symétriques respectifs de
et
par rapport à
, on a :
b.
Comme et
sont les symétriques respectifs de
et
par rapport à
, on a :
c.
Comme est le symétrique de
par rapport à
, on a :
d.
Comme est le symétrique de
par rapport à
, on a :
2. Que peut-on dire des droites :
a. et
?
Propriété :
La symétrie centrale transforme une droite en une autre droite qui lui est parallèle.
Les droites et
sont symétriques par rapport à
, donc elles sont parallèles :
b. et
?
Les droites et
sont confondues par la symétrie centrale par rapport à
:
Exercice 12 : utiliser les propriétés de la symétrie
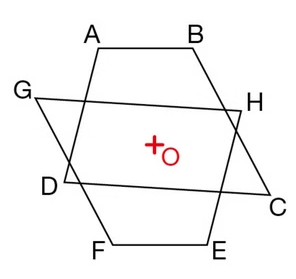
En effet, les quadrilatères et
sont symétriques par rapport au point
.
Propriété :
La symétrie centrale transforme une droite en une autre droite qui lui est parallèle.
Les droites et
sont parallèles.
En particulier, le point est symétrique du point
par rapport à
, et le point
est symétrique du point
par rapport à
.
Ainsi, les segments et
sont symétriques par rapport à
. Par la propriété de la symétrie centrale, deux segments symétriques par rapport à un point sont parallèles.
Donc, les droites et
sont parallèles.
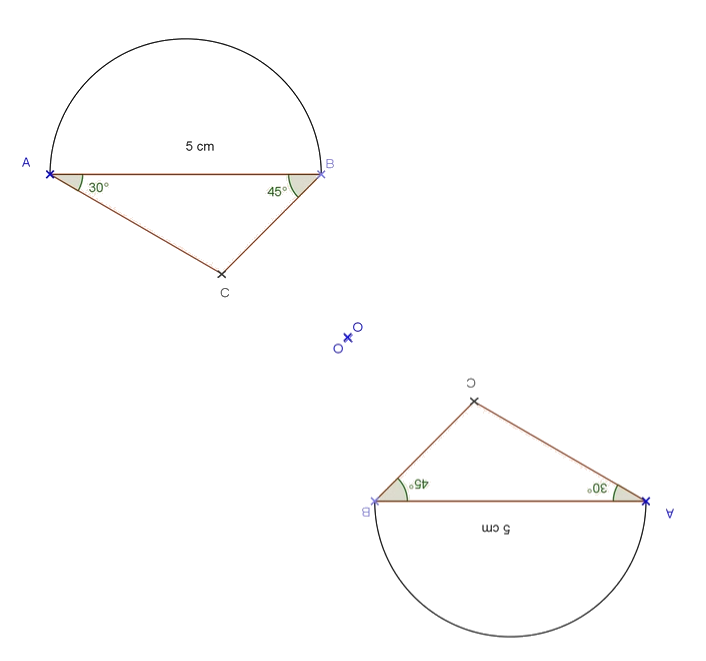
Exercice 13 : les propriétés de la symétrie centrale.
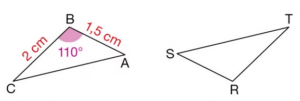
Les triangles et
sont symétriques par rapport au point
.
Les longueurs des côtés correspondants sont égales :
L’angle au sommet est égal à celui au sommet
, donc :
Exercice 14 : utilisation des propriétés de la symétrie centrale.
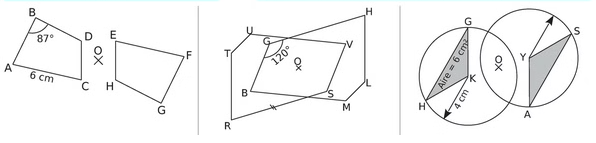
Pour chaque figure symétrique, nous allons appliquer les propriétés de la symétrie centrale pour justifier les réponses.
1. Première figure (quadrilatères BCDE et FGHI) :
– D’après la propriété 1 (« La symétrie centrale conserve les longueurs »), les segments ,
, et
sont égaux.
– On peut aussi observer que les angles sont conservés par la symétrie centrale (propriété 4). Ainsi, l’angle .
2. Deuxième figure (triangle ABC et triangle DEF) :
– La symétrie centrale conserve les longueurs (propriété 1), ce qui implique .
– On peut aussi observer que les angles sont conservés par la symétrie centrale (propriété 4). Ainsi, l’angle .
3. Troisième figure (quadrilatères LMNO et PQRS) :
– La symétrie centrale conserve les longueurs (propriété 1), ainsi les rayons des cercles sont les mêmes.
– L’aire des figures est conservée par la symétrie centrale (propriété 4), donc l’aire du triangle GHK est égale à l’aire du triangle YSA et elle vaut 6 cm².
Exercice 15 : construire le symétrique de la figure.
Exercice 16 : construire le symétrique en utilisant le quadrillage
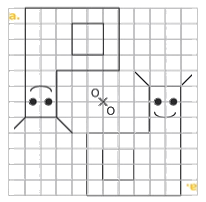
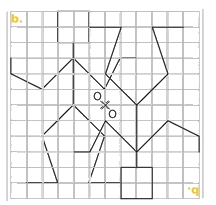
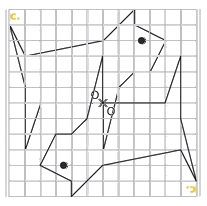
Exercice 17 : construire le symétrique de la tête
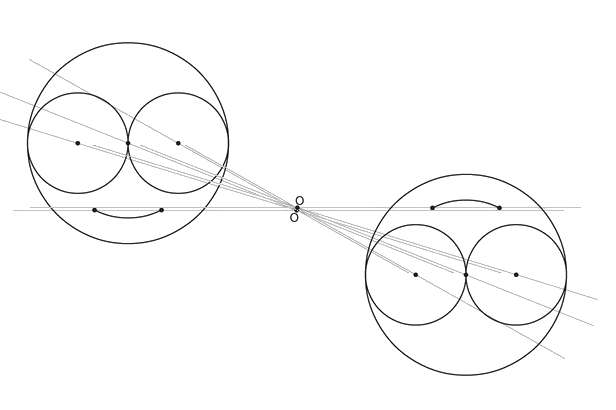
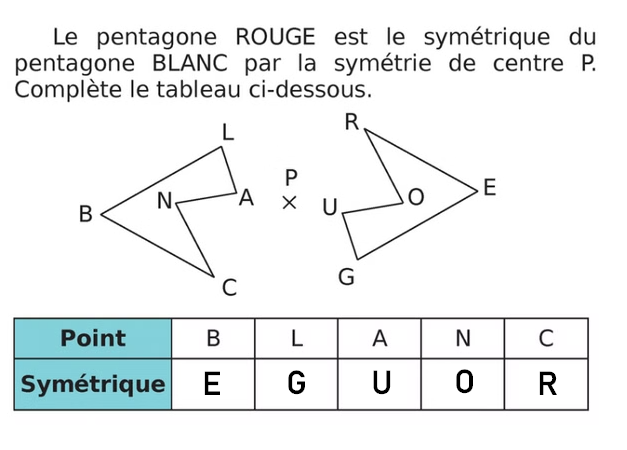
Exercice 18 : quel est le point symétrique ?
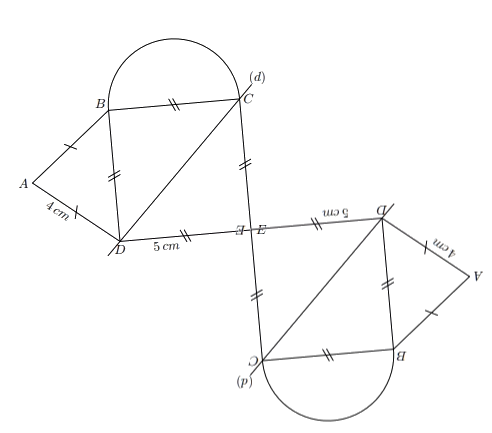
Exercice 19 : tracer le symétrique de cette figure
Exercice 20 : utilisation des propriétés de la symétrie centrale
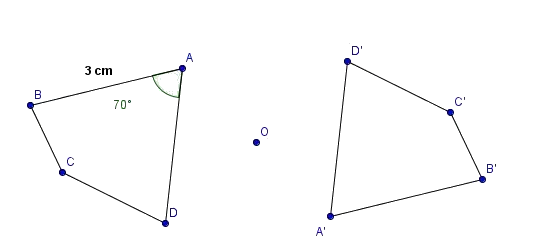
1. Quelle est la longueur du segment [A’B’]? Justifier.
Le point A’ est le symétrique du point A et le point B’ est le symétrique du point B.
Puisque la symétrie conserve les longueurs, la longueur du segment [A’B’] est égale à la longueur du segment [AB].
Sachant que le segment [AB] mesure 3 cm, on a :
2. Quelle est la mesure de l’angle ? Justifier.
La symétrie par rapport à O conserve les mesures des angles.
Donc, l’angle a la même mesure que l’angle
.
Sachant que l’angle , on a :
Réviser les cours et exercices de maths avec nos Q.C.M :
D'autres outils pour progresser en autonomie :